adsense
Học Bài 2. Các phép biến đổi lượng giác – Toán 11 – CD
==============
Lý thuyết
I. Công thức cộng
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a – b} \right) = \sin a\cos b – \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b – \sin asinb\\\cos \left( {a – b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}}\\\tan \left( {a – b} \right) = \frac{{\tan a – \tan b}}{{1 + \tan a\tan b}}\end{array}\)
II. Công thức nhân đôi
\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a – {\sin ^2}a = 2{\cos ^2}a – 1 = 1 – 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 – {{\tan }^2}a}}\end{array}\)
Suy ra, công thức hạ bậc:
\({\sin ^2}a = \frac{{1 – \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)
III. Công thức biến đổi tích thành tổng
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a – b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a – b} \right) – \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a – b} \right)} \right]\end{array}\)
IV. Công thức biến đổi tổng thành tích
\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a – b}}{2}\\\cos a – \cos b = – 2\sin \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a – b}}{2}\\\sin a – \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\end{array}\)
Giải mục 1 trang 16, 17 SGK Toán 11 tập 1 – Cánh Diều
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 1
Cho tam giác MNP có đường cao PQ (Hình 17).
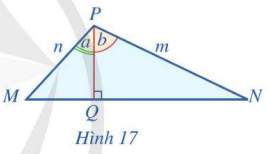
a) Viết công thức tính PQ theo cạnh n và góc a; công thức tính PQ theo cạnh m và góc b
b) Viết công thức tính diện tích mỗi tam giác MPQ, NPQ, MNP theo các cạnh m, n và các cạnh m, n và các góc a, b, a + b
c) Sử dụng kết quả: \({S_{MPN}} = {S_{MPQ}} + {S_{NPQ}}\), hãy tìm công thức tính \(\sin \left( {a + b} \right)\) theo \(\sin a,\cos a,\sin b,\cos b\). Từ đó rút ra đẳng \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b\,\,\,\left( * \right)\)
d) Tính \(\sin \left( {a – b} \right)\) bằng cách biến đổi \(\sin \left( {a – b} \right) = \sin \left[ {a + \left( { – b} \right)} \right]\) và sử dụng công thức (*)
Phương pháp giải:
Dựa vào công thức sin, cos đã học để xác định
Lời giải chi tiết:
a) \(PQ = n.\cos a,PQ = m.\cos b\)
b) \(MQ = n.\sin a,PN = m.\sin b \Rightarrow MN = n.\sin a + m.\sin b\)
\(\begin{array}{l}{S_{MPQ}} = \frac{1}{2}m.\cos b.n.\sin a = \frac{1}{2}m.n.\cos b.\sin a\\{S_{NPQ}} = \frac{1}{2}n.\cos a.m.\sin b = \frac{1}{2}m.n.\cos a.\sin b\\{S_{MNP}} = \frac{1}{2}m.n.\sin \left( {a + b} \right)\end{array}\)
c) \({S_{MNP}} = {S_{MPQ}} + {S_{NPQ}} \Rightarrow \frac{1}{2}m.n.\cos b.\sin a + \frac{1}{2}m.n.\cos a.\sin b = \frac{1}{2}m.n.\sin \left( {a + b} \right)\)
\( \Rightarrow \sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\)
d) \(\sin \left( {a – b} \right) = \sin \left[ {a + \left( { – b} \right)} \right] = \sin a.\cos \left( { – b} \right) + \cos a.\sin \left( { – b} \right) = \sin a.\cos b – \cos a.\sin b\)
Luyện tập – Vận dụng
Tính \(\sin \frac{\pi }{{12}}\)
Phương pháp giải:
Sử dụng công thức cộng đối với sin
Lời giải chi tiết:
Áp dụng công thức cộng, ta có:
\(\begin{array}{l}\sin \frac{\pi }{{12}} = \sin \left( {\frac{\pi }{4} – \frac{\pi }{6}} \right) = \sin \frac{\pi }{4}.\cos \frac{\pi }{6} – \cos \frac{\pi }{4}.\sin \frac{\pi }{6}\\ = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} – \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 – \sqrt 2 }}{4}\end{array}\)
Hoạt động 2
a) Tính \(\cos \left( {a + b} \right)\) bằng cách biến đổi \(\cos \left( {a + b} \right) = \sin \left[ {\frac{\pi }{2} – \left( {a + b} \right)} \right] = \sin \left[ {\left( {\frac{\pi }{2} – a} \right) – b} \right]\) và sử dụng công thức cộng đối với sin
b) Tính \(\cos \left( {a – b} \right)\) bằng cách biến đổi \(\cos \left( {a – b} \right) = \cos \left[ {a + \left( { – b} \right)} \right]\) và sử dụng công thức \(\cos \left( {a + b} \right)\) có được ở câu a
Phương pháp giải:
Dựa vào công thức cộng sin đã chứng minh ở bên trên để tính
Lời giải chi tiết:
a) \(\cos \left( {a + b} \right) = \sin \left[ {\left( {\frac{\pi }{2} – a} \right) – b} \right] = \sin \left( {\frac{\pi }{2} – a} \right).\cos b – \cos \left( {\frac{\pi }{2} – a} \right).\sin b = \cos a.\cos b – \sin a.\sin b\)
b) \(\cos \left( {a – b} \right) = \cos \left[ {a + \left( { – b} \right)} \right] = \cos a.\cos \left( { – b} \right) – \sin a.\sin \left( { – b} \right) = \sin a.\sin b + \cos a.\cos b\)
Luyện tập – Vận dụng 2
Tính \(\cos {15^ \circ }\)
Phương pháp giải:
Sử dụng công thức cộng dối với cosin
Lời giải chi tiết:
Áp dụng công thức cộng, ta có:
\(\begin{array}{l}\cos {15^ \circ } = \cos ({45^ \circ } – {30^ \circ }) = \cos {45^ \circ }\cos {30^ \circ } + \sin {45^ \circ }\sin {30^ \circ }\\ = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\end{array}\)
Hoạt động 3
a) Sử dụng công thức cộng đối với sin và côsin, hãy tính \(\tan \left( {a + b} \right)\) theo tan a và tan b khi các biểu thức đều có nghĩa
b) Khi các biểu thức đều có nghĩa, hãy tính \(\tan \left( {a – b} \right)\) bằng cách biến đổi \(\tan \left( {a – b} \right) = \tan \left[ {a + \left( { – b} \right)} \right]\) và sử dụng công thức \(\tan \left( {a + b} \right)\) có được ở câu a.
Phương pháp giải:
Dựa vào công thức cộng sin, cos đã chứng minh ở bên trên để tính
Lời giải chi tiết:
a) \(\tan \left( {a + b} \right) = \frac{{\sin \left( {a + b} \right)}}{{\cos \left( {a + b} \right)}} = \frac{{\sin a.\cos b + \cos a.\sin b}}{{\cos a.\cos b – \sin a.\sin b}}\)
\(\begin{array}{l} = \frac{{\sin a.\cos b + \cos a.\cos b}}{{\cos a.\cos b – \sin a.\sin b}} = \frac{{\sin a.\cos b}}{{\cos a.\cos b – \sin a.\sin b}} + \frac{{\cos a.\sin b}}{{\cos a.\cos b – \sin a.\sin b}}\\ = \frac{{\frac{{\sin a.\cos b}}{{\cos a.\cos b}}}}{{\frac{{\cos a.\cos b – \sin a.\sin b}}{{\cos a.\cos b}}}} + \frac{{\frac{{\cos a.\sin b}}{{\cos a.\cos b}}}}{{\frac{{\cos a.\cos b – \sin a.\sin b}}{{\cos a.\cos b}}}} = \frac{{\tan a}}{{1 – \tan a.\tan b}} + \frac{{\tan b}}{{1 – \tan a.\tan b}}\\ = \frac{{\tan a + \tan b}}{{1 – \tan a.\tan b}}\end{array}\)
\( \Rightarrow \tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a.\tan b}}\)
b)
adsense
\(\tan \left( {a – b} \right) = \tan \left( {a + \left( { – b} \right)} \right) = \frac{{\tan a + \tan \left( { – b} \right)}}{{1 – \tan a.\tan \left( { – b} \right)}} = \frac{{\tan a – \tan b}}{{1 + \tan a.\tan b}}\)
Luyện tập – Vận dụng
Tính \(\tan {165^ \circ }\)
Phương pháp giải:
Sử dụng công thức cộng đối với tang
Lời giải chi tiết:
\(\begin{array}{l}\tan {165^ \circ } = \tan ({105^ \circ } + {60^ \circ }) = \frac{{\tan {{105}^ \circ } + \tan {{60}^ \circ }}}{{1 – \tan {{105}^ \circ }.\tan {{60}^ \circ }}}\\ = \frac{{ – 2 – \sqrt 3 + \sqrt 3 }}{{1 – ( – 2 – \sqrt 3 ).\sqrt 3 }} = – 2 + \sqrt 3 \end{array}\)
Giải mục 2 trang 18 SGK Toán 11 tập 1 – Cánh Diều
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 4
Tính \(\sin 2a,\,\,\cos 2a,\,\,\tan 2a\) bằng cách thay \(b = a\) trong công thức cộng.
Phương pháp giải:
Dựa vào công thức cộng để khai triển
Lời giải chi tiết:
\(\sin 2a = \sin \left( {a + a} \right) = \sin a.\cos a + \cos a.\sin a = 2\sin a\cos a\)
\(\begin{array}{l}\cos 2a = \cos \left( {a + a} \right) = \cos a.\cos a – \sin a.\sin a = {\cos ^2}a – {\sin ^2}a\\\tan 2a = \tan \left( {a + a} \right) = \frac{{\tan a + \tan a}}{{1 – \tan a.\tan a}} = \frac{{2\tan a}}{{1 – {{\tan }^2}a}}\end{array}\)
Luyện tập – Vận dụng
Cho \(\tan \frac{\alpha }{2} = – 2\). Tính \(\tan \alpha \)
Phương pháp giải:
Sử dụng công thức nhân đôi
Lời giải chi tiết:
Áp dụng công thức nhân đôi ta có:
\(\tan \alpha = \frac{{2.\tan \frac{\alpha }{2}}}{{1 – {{\tan }^2}\frac{\alpha }{2}}} = \frac{{2.( – 2)}}{{1 – {{( – 2)}^2}}} = \frac{4}{3}\)
Luyện tập – Vận dụng
Tính \(\sin \frac{\pi }{8};\cos \frac{\pi }{8}\)
Phương pháp giải:
Sử dụng công thức hạ bậc
Lời giải chi tiết:
Ta có : \({\sin ^2}\frac{\pi }{8} = \frac{{1 – \cos \frac{\pi }{4}}}{2} = \frac{{2 – \sqrt 2 }}{4}\)
Mà \(\sin \frac{\pi }{8} > 0\) nên \(\sin \frac{\pi }{8} = \frac{{\sqrt {2 – \sqrt 2 } }}{2}\)
Ta có : \({\cos ^2}\frac{\pi }{8} = \frac{{1 + \cos \frac{\pi }{4}}}{2} = \frac{{2 + \sqrt 2 }}{4}\)
Mà \(\cos \frac{\pi }{8} > 0\) nên \(\cos \frac{\pi }{8} = \frac{{\sqrt {2 + \sqrt 2 } }}{2}\)
Giải mục 3 trang 18, 19 SGK Toán 11 tập 1 – Cánh Diều
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động
Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:
\(\cos \left( {a + b} \right) + \cos \left( {a – b} \right);\,\,\cos \left( {a + b} \right) – \cos \left( {a – b} \right);\,\,\sin \left( {a + b} \right) + \sin \left( {a – b} \right)\)
Phương pháp giải:
Dựa vào công thức cộng đã học để triển khai:
Lời giải chi tiết:
\(\begin{array}{l}\cos \left( {a + b} \right) + \cos \left( {a – b} \right) = \cos a.\cos b – \sin a.\sin b + \sin a.\sin b + \cos a.\cos b = 2\cos a.\cos b\\\cos \left( {a + b} \right) – \cos \left( {a – b} \right) = \cos a.\cos b – \sin a.\sin b – \sin a.\sin b – \cos a.\cos b = – 2\sin a.\sin b\\\sin \left( {a + b} \right) + \sin \left( {a – b} \right) = \sin a.\cos b + \cos a.\sin b + \sin a.\cos b – \cos a.\sin b = 2\sin a.\cos b\end{array}\)
Luyện tập – Vận dụng
Cho \(\cos \alpha = \frac{2}{3}\).
Tính \(B = \cos \frac{{3\alpha }}{2}.\cos \frac{\alpha }{2}\)
Phương pháp giải:
Sử dụng công thức biến đổi tích thành tổng
Lời giải chi tiết:
Ta có :
\(\begin{array}{l}B = \cos \frac{{3\alpha }}{2}.\cos \frac{\alpha }{2} = \frac{1}{2}\left[ {\cos \left( {\frac{{3\alpha }}{2} + \frac{\alpha }{2}} \right) + \cos \left( {\frac{{3\alpha }}{2} – \frac{\alpha }{2}} \right)} \right]\\ = \frac{1}{2}\left[ {\cos (2\alpha ) + \cos \alpha } \right] = \frac{1}{2}\left[ {2.{{\cos }^2}\alpha – 1 + \cos \alpha } \right] = \frac{1}{2}\left[ {2.{{\left( {\frac{2}{3}} \right)}^2} – 1 + \frac{2}{3}} \right] = \frac{5}{{18}}\end{array}\)
Giải mục 4 trang 19, 20 SGK Toán 11 tập 1 – Cánh Diều
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 6
Sử dụng công thức biến đổi tích thành tổng và đặt \(a + b = u;\,\,a – b = v\) biến đổi các biểu thức sau thành tích: \(\cos u + \cos v;\,\,\cos u – \cos v;\,\,\sin u + \sin v;\,\,\sin u – \sin v\)
Phương pháp giải:
Dựa vào công thức biến tích thành tổng để biến đổi:
Lời giải chi tiết:
\(\begin{array}{l}1.\,\,\,\,\cos a.\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a – b} \right)} \right] \Leftrightarrow 2\cos a.\cos b = \cos \left( {a + b} \right) + \cos \left( {a – b} \right)\\ \Leftrightarrow 2\cos \frac{{u + v}}{2}.\cos \frac{{u – v}}{2} = \cos u + \cos v\\2.\,\,\,\,\sin a.\sin b = – \frac{1}{2}.\left[ {\cos \left( {a + b} \right) – \cos \left( {a – b} \right)} \right] \Leftrightarrow – 2.\sin a.\sin b = \cos \left( {a + b} \right) – \cos \left( {a – b} \right)\\ \Leftrightarrow – 2.\sin \frac{{u + v}}{2}.\sin \frac{{u – v}}{2} = \cos u – \cos v\\3.\,\,\,\,\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a – b} \right)} \right] \Leftrightarrow 2\sin a.\cos b = \sin \left( {a + b} \right) + \sin \left( {a – b} \right)\\ \Leftrightarrow 2\sin \frac{{u + v}}{2}.\cos \frac{{u – v}}{2} = \sin u + \sin v\\4.\,\,\,\,\sin \left( {a + b} \right) – \sin \left( {a – b} \right) = \sin a.\cos b + \cos a.\sin b – \sin a.\cos b + \cos a.\sin b = 2\cos a.\sin b\\ \Leftrightarrow \sin u – \sin v = 2.\cos \frac{{u + v}}{2}.\sin \frac{{u – v}}{2}\end{array}\)
Luyện tập – Vận dụng
Tính \(D = \frac{{\sin \frac{{7\pi }}{9} + \sin \frac{\pi }{9}}}{{\cos \frac{{7\pi }}{9} – \cos \frac{\pi }{9}}}\)
Phương pháp giải:
Sử dụng công thức biến đổi tổng thành tích
Lời giải chi tiết:
Ta có:
\(D = \frac{{\sin \frac{{7\pi }}{9} + \sin \frac{\pi }{9}}}{{\cos \frac{{7\pi }}{9} – \cos \frac{\pi }{9}}} = \frac{{2.\sin \left( {\frac{{\frac{{7\pi }}{9} + \frac{\pi }{9}}}{2}} \right).\cos \left( {\frac{{\frac{{7\pi }}{9} – \frac{\pi }{9}}}{2}} \right)}}{{ – 2.\sin \left( {\frac{{\frac{{7\pi }}{9} + \frac{\pi }{9}}}{2}} \right).\sin \left( {\frac{{\frac{{7\pi }}{9} – \frac{\pi }{9}}}{2}} \right)}} = \cot \frac{\pi }{3} = \frac{{\sqrt 3 }}{3}\)
