adsense
LÝ THUYẾT Bài 2. Công thức lượng giác Toán 11 kết nối tri thức
=======================
Lý thuyết Công thức lượng giác – SGK Toán 11 Kết nối tri thức
1. Công thức cộng
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a – b} \right) = \sin a\cos b – \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b – \sin asinb\\\cos \left( {a – b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}}\\\tan \left( {a – b} \right) = \frac{{\tan a – \tan b}}{{1 + \tan a\tan b}}\end{array}\)
2. Công thức nhân đôi
\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a – {\sin ^2}a = 2{\cos ^2}a – 1 = 1 – 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 – {{\tan }^2}a}}\end{array}\)
Suy ra, công thức hạ bậc:
\({\sin ^2}a = \frac{{1 – \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)
3. Công thức biến đổi tích thành tổng
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a – b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a – b} \right) – \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a – b} \right)} \right]\end{array}\)
4. Công thức biến đổi tổng thành tích
\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a – b}}{2}\\\cos a – \cos b = – 2\sin \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a – b}}{2}\\\sin a – \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\end{array}\)
Giải mục 2 trang 18, 19 SGK Toán 11 tập 1 – Kết nối tri thức
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 2
Lấy b = a trong các công thức cộng, hãy tìm công thức tính: \(\sin 2a;\cos 2a;\tan 2a\).
Phương pháp giải:
Sử dụng công thức cộng lượng giác
Lời giải chi tiết:
\(\sin 2a = \sin \left( {a + a} \right) = \sin \left( {a + b} \right) = \sin a\cos b + \sin b\cos a = 2\sin a\cos a\)
\(\cos 2a = \cos \left( {a + a} \right) = \cos \left( {a + b} \right) = \cos a\cos b – \sin a\sin b = {\cos ^2}a – {\sin ^2}a = 2{\cos ^2}a – 1\)
\( = 1 – 2{\sin ^2}a\)
\(\tan 2a = \tan \left( {a + a} \right) = \tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}} = \frac{{2\tan a}}{{1 – {{\tan }^2}a}}\)
Luyện tập 2
Không dùng máy tính, tính \(\cos \frac{\pi }{8}\)
Phương pháp giải:
Sử dụng công thức hạ bậc \({\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)
Lời giải chi tiết:
Ta có: \({\cos ^2}\frac{\pi }{8} = \frac{{1 + \cos \frac{\pi }{4}}}{2} = \frac{{1 + \frac{{\sqrt 2 }}{2}}}{2} = \frac{{2 – \sqrt 2 }}{4}\)
Suy ra: \(\cos \frac{\pi }{8} = \frac{1}{2}\sqrt {2 + \sqrt 2 } \)
Giải mục 3 trang 19 SGK Toán 11 tập 1 – Kết nối tri thức>
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 3
a) Từ các công thức cộng \(\cos \left( {a + b} \right)\) và \(\cos \left( {a – b} \right)\), hãy tìm: \(\cos a\cos b;\sin a\sin b\).
b) Từ các công thức cộng \(\sin \left( {a + b} \right)\) và \(\sin \left( {a – b} \right)\), hãy tìm: \(\sin a\cos b\).
Lời giải chi tiết:
a) Ta có: \(\cos \left( {a + b} \right) + \cos \left( {a – b} \right) = \cos a\cos b + \sin a\sin b + \cos a\cos b – \sin a\sin b = 2\cos a\cos b\)
Suy ra: \(\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a – b} \right) + \cos \left( {a + b} \right)} \right]\;\)
b) Ta có: \(\sin \left( {a + b} \right) + \sin \left( {a – b} \right) = \sin a\cos b + \cos a\sin b + \sin a\cos b – \cos a\sin b = 2\sin a\cos b\)
Suy ra: \(\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a – b} \right) + \sin \left( {a + b} \right)} \right]\)
Luyện tập 3
Không dùng máy tính, tính giá trị của các biểu thức:
adsense
\(A = \cos {75^0}\cos {15^0}\);
\(B = \sin \frac{{5\pi }}{{12}}\cos \frac{{7\pi }}{{12}}\).
Phương pháp giải:
Áp dụng công thức:
\(\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a – b} \right) + \cos \left( {a + b} \right)} \right]\)
\(\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a – b} \right) + \sin \left( {a + b} \right)} \right]\)
Lời giải chi tiết:
\(A = \cos {75^0}\cos {15^0} = \frac{1}{2}\left[ {\cos \left( {{{75}^0} – {{15}^0}} \right) + \cos \left( {{{75}^0} + {{15}^0}} \right)} \right] = \frac{1}{2}.\cos {60^0}.\cos {90^0} = 0\)
\(B = \sin \frac{{5\pi }}{{12}}\cos \frac{{7\pi }}{{12}} = \frac{1}{2}\left[ {\sin \left( {\frac{{5\pi }}{{12}} – \frac{{7\pi }}{{12}}} \right) + \sin \left( {\frac{{5\pi }}{{12}} + \frac{{7\pi }}{{12}}} \right)} \right] = \frac{1}{2}\sin \left( { – \frac{{2\pi }}{{12}}} \right).\sin \left( {\frac{{12\pi }}{{12}}} \right) = – \frac{1}{2}\sin \frac{\pi }{6}\sin \pi = 0\)
Giải mục 4 trang 20 SGK Toán 11 tập 1 – Kết nối tri thức>
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 4
Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt \(u = a – b,\;v = a + b\) và viết các công thức nhận được
Lời giải chi tiết:
Ta có: \(u = a – b;v = a + b\).
Suy ra \(u + v = 2a \to a = \frac{{u + v}}{2}\)
\(u – v = 2b \to b = \frac{{u – v}}{2}\)
Ta có: \(\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u – v}}{2}\)
\(\cos u – \cos v = – 2\sin \frac{{u + v}}{2}\sin \frac{{u – v}}{2}\)
\(\sin u + \sin v = 2\sin \frac{{u + v}}{2}\cos \frac{{u – v}}{2}\)
\(\sin u – \sin v = 2\cos \frac{{u + v}}{2}\sin \frac{{u – v}}{2}\)
Luyện tập 4
Không dùng máy tính, tính giá trị của biểu thức
\(B = \cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9} + \cos \frac{{11\pi }}{9}\).
Phương pháp giải:
Sử dụng công thức: \(\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u – v}}{2}\)
Lời giải chi tiết:
\(B = \left( {\cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9}} \right) + \cos \frac{{11\pi }}{9} = \left( {2\cos \frac{{\frac{\pi }{9} + \frac{{5\pi }}{9}}}{2}\cos \frac{{\frac{\pi }{9} – \frac{{5\pi }}{9}}}{2}} \right) + \cos \frac{{11\pi }}{9} = 2\cos \frac{\pi }{3}\cos \frac{{2\pi }}{9} + \cos \frac{{11\pi }}{9}\)
\( = \cos \frac{{2\pi }}{9} + \cos \frac{{11\pi }}{9} = 2\cos \frac{{\frac{{2\pi }}{9} + \frac{{11\pi }}{9}}}{2}\cos \frac{{\frac{{2\pi }}{9} – \frac{{11\pi }}{9}}}{2} = 2\cos \frac{{13\pi }}{{18}}\cos \frac{\pi }{2} = 0\)
Vận dụng
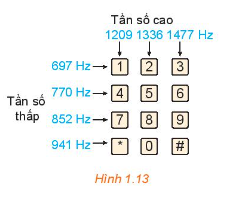
Khi nhấn một phím trên điện thoại cảm ứng, bàn phím sẽ tạo ra hai âm thuần, kết hợp với nhau để tạo ra âm thanh nhận dạng duy nhất phím. Hình 1.13 cho thấy tần số thấp \({f_1}\) và tần số cao \({f_2}\) liên quan đến mỗi phím. Nhấn một phím sẽ tạo ra sóng âm \(y = \sin \left( {2\pi {f_1}t} \right) + \sin \left( {2\pi {f_2}t} \right)\), ở đó t là biến thời gian (tính bằng giây).
a) Tìm hàm số mô hình hóa âm thanh được tạo ra khi nhấn phím 4.
b) Biến đổi công thức vừa tìm được ở câu a về dạng tích của một hàm số sin và một hàm số côsin.
Phương pháp giải:
Sử dụng công thức: \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\)
Lời giải chi tiết:
a) Khi nhấn phím 4, ta có sóng âm \(y = \sin \left( {2\pi .770t} \right) + \sin \left( {2\pi .1209t} \right)\)
b) Ta có: \(\sin \left( {2\pi .770t} \right) + \sin \left( {2\pi .1209t} \right) = 2\sin \frac{{2\pi .770t + 2\pi .1209t}}{2}\cos \frac{{2\pi .770t – 2\pi .1209t}}{2}\)
\( = – 2.\sin 1979\pi t.\sin 439\pi t\)
