Trong không gian Oxyz, tập hợp các điểm thỏa mãn (left| x right| + left| y right| + left| z right| le 2) và (left| {x – 2} right| + left| y right| + left| z right| le 2) là một khối đa diện có thể tích bằng:
Lời giải tham khảo:
Đáp án đúng: D
Có (0 le left| x right| + left| y right| + left| z right| le 2) và (0 le left| {x – 2} right| + left| y right| + left| z right| le 2) nên tìm các điểm đầu mút.
(left| x right| + left| y right| + left| z right| = 0 Rightarrow x = y = z = 0 Rightarrow Oleft( {0;0;0} right)).
(left| {x – 2} right| + left| y right| + left| z right| = 0 Rightarrow x = 2;y = z = 0 Rightarrow Aleft( {2;0;0} right)).
Xét hệ phương trình (left{ begin{array}{l}left| x right| + left| y right| + left| z right| = 2\left| {x – 2} right| + left| y right| + left| z right| = 2end{array} right. Rightarrow left| x right| = left| {x – 2} right| Leftrightarrow x = 2 – x Leftrightarrow x = 1)
( Rightarrow left| y right| + left| z right| = 1 Rightarrow left[ begin{array}{l}y = 0;,,z = pm 1\y = pm 1;,,z = 0end{array} right.) ( Rightarrow Bleft( {1;0;1} right),B’left( {1;0; – 1} right),Cleft( {1;1;0} right),C’left( {1; – 1;0} right))
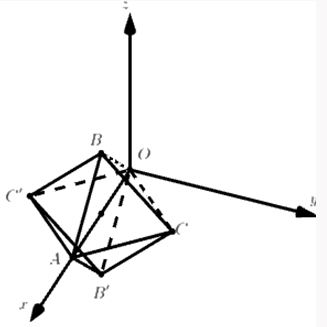
Dựng hình suy ra tập hợp các điểm thảo mãn là bát diện (B.OCAC’.B’)
Ta có (OB = sqrt {{1^2} + {1^2}} = sqrt 2 ), do đó hình bát diện đều (B.OCAC’.B’) có cạnh bằng (sqrt 2 ).
Vậy thể tích của bát diện đều là (V = frac{{{{left( {sqrt 2 } right)}^3}sqrt 2 }}{3} = frac{4}{3}).
Chọn D.
