Bài tập nhận dạng đồ thị hàm số bậc ba có đáp án
Dưới đây là một số bài tập trắc nghiệm nhận dạng đồ thị hàm số có đáp án chi tiết
|
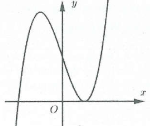
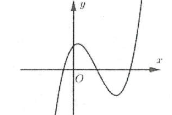
Bài tập 1: [Đề THPT QG năm 2017] Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây? A. $y={{x}^{3}}-3{{x}^{2}}+2$. B. $y={{x}^{4}}-{{x}^{2}}+1$. C. $y={{x}^{4}}+{{x}^{2}}+1$. D. $y=-{{x}^{3}}+3{{x}^{2}}+2$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy
Hàm số đã cho có 2 điểm cực trị nên ta loại đáp án B và C.
Mặt khác $underset{xto +infty }{mathop{lim }},y=+infty $ nên hệ số. Chọn A.
|
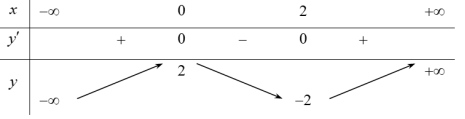
Bài tập 2: Cho hàm số $y=fleft( x right)$ liên tục trên $mathbb{R}$ và có bảng biến thiên như hình vẽ. Hàm số $y=fleft( x right)$ là hàm số nào trong các hàm số sau: A. $y={{x}^{3}}-3{{x}^{2}}+2$. B. $y=-{{x}^{3}}+3{{x}^{2}}+2$. C. $y=-{{x}^{3}}-3{{x}^{2}}+2$. D. $y={{x}^{3}}+3{{x}^{2}}+2$. |
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy
$underset{xto +infty }{mathop{lim }},y=+infty Rightarrow $ Hệ số $a>0$ do đó loại B và C.
Mặt khác hàm số đạt cực trị tại $x=0,,x=2$ nên loại D. Chọn A.
|
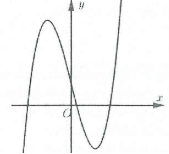
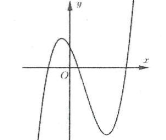
Bài tập 3: Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây? A. $y={{x}^{3}}-4x+1$. B. $y={{x}^{3}}+3{{x}^{2}}+1$. C. $y={{x}^{3}}-4x-1$. D. $y=-{{x}^{3}}+4x+1$. |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy
Đồ thị hàm số cắt trục tung tại điểm $left( 0;d right)Rightarrow d>0$ nên ta loại đáp án C
$underset{xto +infty }{mathop{lim }},y=+infty Rightarrow a>0$ nên ta loại đáp án D.
Mặt khác hàm số đạt cực trị tại hai điểm ${{x}_{1}},,{{x}_{2}}$ dựa vào hình vẽ ta thấy ${{x}_{1}},,{{x}_{2}}$ trái dấu nên đáp án ta loại đáp án B. Chọn A.
|
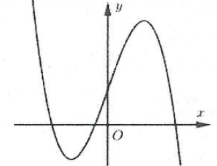
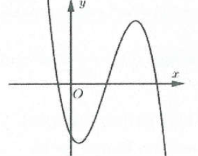
Bài tập 4: Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. $y=-{{x}^{3}}+3{{x}^{2}}+1$. B. $y=-{{x}^{3}}+3x+1$. C. $y={{x}^{3}}-3x+1$. D. $y=-{{x}^{3}}-3x+1$. |
Lời giải chi tiết
Hàm số có hệ số $a<0$ do $underset{xto +infty }{mathop{lim }},y=-infty $ nên loại đáp án C.
Hàm số có 2 điểm cực trị ${{x}_{1}}<0<,{{x}_{2}}$ nên ${y}’=0$ có 2 nghiệm phân biệt trái dấu.
Xét đáp án A. $y=-{{x}^{3}}+3{{x}^{2}}+1Rightarrow {y}’=-3{{x}^{2}}+6x=0Leftrightarrow left[ begin{array} {} x=0 \ {} x=2 \ end{array} right.$ (loại).
Xét đáp án D. $y=-{{x}^{3}}-3x+1Rightarrow {y}’=-3{{x}^{2}}-3x<0left( forall xin mathbb{R} right)$ (loại). Chọn B.
|
Bài tập 5: Đường cong hình bên là đồ thị của hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$. Khẳng định nào sau đây là đúng? A. $a>0,,b0,,d>0$. B. $a>0,,b<0,,c0$. C. $a>0,,b>0,,c0$. D. $a>0,,b>0,,c>0,,d<0$. |
Lời giải chi tiết
Dựa vào đồ thị ta thấy: $underset{xto +infty }{mathop{lim }},y=+infty Rightarrow a>0$; đồ thị hàm số đi qua điểm $left( 0;d right)Rightarrow d>0$.
Hàm số đạt cực trị tại hai điểm ${{x}_{1}},,,{{x}_{2}}$ dựa vào hình vẽ ta thấy ${{x}_{1}}>0,,,{{x}_{2}}>0$
Mặt khác: ${y}’=3a{{x}^{2}}+2bx+cRightarrow left{ begin{array} {} {{x}_{1}}+{{x}_{2}}=frac{-2b}{3a}>0xrightarrow{a>0}b<0 \ {} {{x}_{1}}{{x}_{2}}=frac{c}{3a}>0xrightarrow{a>0}c>0 \ end{array} right.$. Chọn A.
|
Bài tập 6: Đường cong hình bên là đồ thị của hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$. Khẳng định nào sau đây là đúng? A. $a>0,,b0,,d>0$. B. $a>0,,b<0,,c0$. C. $a>0,,b>0,,c0$. D. $a0,,c>0,,d<0$. |
Lời giải chi tiết
Dựa vào đồ thị ta thấy: $underset{xto +infty }{mathop{lim }},y=+infty Rightarrow a>0$; đồ thị hàm số đi qua điểm $left( 0;d right)Rightarrow d>0$.
Hàm số đạt cực trị tại hai điểm ${{x}_{1}},,,{{x}_{2}}$ dựa vào hình vẽ ta thấy ${{x}_{1}}0$ và ${{x}_{1}}+{{x}_{2}}>0$
Mặt khác: ${y}’=3a{{x}^{2}}+2bx+cRightarrow left{ begin{array} {} {{x}_{1}}+{{x}_{2}}=frac{-2b}{3a}>0xrightarrow{a>0}b<0 \ {} {{x}_{1}}{{x}_{2}}=frac{c}{3a}0}c<0 \ end{array} right.$. Chọn B.
|
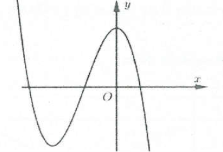
Bài tập 7: Đường cong hình bên là đồ thị của hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$. Khẳng định nào sau đây là đúng? A. $a<0,,b0,,d<0$. B. $a>0,,b>0,,c<0,,d<0$. C. $a<0,,b<0,,c<0,,d<0$. D. $a0,,c<0,,d<0$. |
Lời giải chi tiết
Dựa vào đồ thị ta thấy: $underset{xto +infty }{mathop{lim }},y=-infty Rightarrow a<0$; đồ thị hàm số đi qua điểm $left( 0;d right)Rightarrow d<0$.
Hàm số đạt cực trị tại hai điểm ${{x}_{1}},,,{{x}_{2}}$ dựa vào hình vẽ ta thấy ${{x}_{1}}>0,,,{{x}_{2}}>0$
Mặt khác: ${y}’=3a{{x}^{2}}+2bx+cRightarrow left{ begin{array} {} {{x}_{1}}+{{x}_{2}}=frac{-2b}{3a}>0xrightarrow{a0 \ {} {{x}_{1}}{{x}_{2}}=frac{c}{3a}>0xrightarrow{a<0}c<0 \ end{array} right.$. Chọn D.
|
Bài tập 8: Đường cong hình bên là đồ thị của hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$. Khẳng định nào sau đây là đúng? A. $a>0,,b=0,,c>0,,d>0$. B. $a0,,d>0$. C. $a<0,,b0$. D. $a0,,c=0,,d>0$. |
Lời giải chi tiết
Dựa vào đồ thị ta thấy: $underset{xto +infty }{mathop{lim }},y=-infty Rightarrow a<0$ (loại đáp án A).
Đồ thị hàm số cắt trục tung tại điểm $left( 0;d right)Rightarrow d>0$
Hàm số có 2 điểm cực trị trong đó $left{ begin{array} {} {{x}_{1}}=0 \ {} {{x}_{2}}<0 \ end{array} right.$ nên ${y}’=0$ có 2 nghiệm thỏa mãn $left{ begin{array} {} {{x}_{1}}=0 \ {} {{x}_{2}}<0 \ end{array} right.$.
Ta có: ${y}’=3a{{x}^{2}}+2bx+cRightarrow {y}’left( 0 right)=0Rightarrow c=0Rightarrow {{x}_{2}}=frac{-2b}{3a}<0Rightarrow b<0$. Chọn C.
|
Bài tập 9: Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có các điểm cực trị thỏa mãn ${{x}_{1}}in left( -1;0 right),,,{{x}_{2}}in left( 1;2 right)$. Biết hàm số đồng biến trên khoảng $left( {{x}_{1}};{{x}_{2}} right)$ đồng thời đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Mệnh đề nào dưới đây là đúng? A. $a0,,c<0,,d<0$. B. $a<0,,b0,,d<0$. C. $a>0,,b>0,,c>0,,d<0$. D. $a0,,c>0,,d<0$. |
Lời giải chi tiết
Dựa vào giả thiết, ta có các nhận xét sau:
– Đồ thị hàm số $y=fleft( x right)$ cắt trục tung tại điểm có tung độ âm $Rightarrow fleft( 0 right)=d<0$
– Hàm số $y=fleft( x right)$ đồng biến trên khoảng $left( {{x}_{1}};{{x}_{2}} right)Rightarrow fleft( {{x}_{1}} right)<fleft( {{x}_{2}} right)Rightarrow {{x}_{1}}$ là điểm cực tiểu và ${{x}_{2}}$ điểm cực đại $Rightarrow {{x}_{CT}}<{{x}_{Ctilde{N}}}Rightarrow $ hệ số $a<0$.
– Ta có ${f}’left( x right)=3a{{x}^{2}}+2bx+c$ có hai nghiệm ${{x}_{1}},,,{{x}_{2}}$ thỏa mãn tổng ${{x}_{1}}+{{x}_{2}}=frac{-2b}{3a}>0Rightarrow b>0$ và tích hai nghiệm ${{x}_{1}}.{{x}_{2}}=frac{c}{3a}0$ vì $left{ begin{array} {} -1<{{x}_{1}}<0 \ {} 1<{{x}_{2}}<2 \ end{array} right.Rightarrow left{ begin{array} {} {{x}_{1}}+{{x}_{2}}>0 \ {} {{x}_{1}}.{{x}_{2}}<0 \ end{array} right.$. Chọn D.