Bài tập nhận dạng đồ thị hàm số chứa dấu trị tuyệt đối có đáp án
Phương pháp giải nhận dạng đồ thị hàm trị tuyệt đối
Mẫu 1: Từ đồ thị hàm số $y=fleft( x right),,left( C right)$ suy ra đồ thị hàm số $y=left| fleft( x right), right|,left( C right)$
Ta có: $y=left| fleft( x right), right|=left{ begin{align} & fleft( x right),,text{khi }fleft( x right)ge 0 \ & -fleft( x right),,text{khi }fleft( x right)<0 \ end{align} right.$. Do đó đồ thị hàm số $y=left| fleft( x right), right|,left( C right)$ gồm hai phần:
– Phần 1: Là phần đồ thị hàm số $left( C right)$ nằm phía bên trên trục hoành.
– Phần 2: Lấy đối xứng phần của $left( C right)$ nằm dưới $Ox$ qua $Ox$
|
Đồ thị hàm số $y=fleft( x right),,left( C right)$ |
Đồ thị hàm số $y=left| fleft( x right), right|,left( C right)$ |
|
|
|
Mẫu 2: Từ đồ thị hàm số $y=fleft( x right),,left( C right)$ suy ra đồ thị hàm số $y=fleft( left| x right| right),,left( {{C}_{1}} right)$
Ta có: $y=fleft( left| x right| right),,=left{ begin{align} & fleft( x right),,text{khi }fleft( x right)ge 0 \ & fleft( -x right),,text{khi }fleft( x right)<0 \ end{align} right.$. Do đó đồ thị hàm số $y=fleft( left| x right| right),,left( {{C}_{1}} right)$ gồm hai phần:
– Phần 1: Là phần đồ thị hàm số $left( C right)$ nằm bên phải trục tung.
– Phần 2: Lấy đối xứng phần 1 qua trục tung (vì hàm số $y=fleft( left| x right| right),$ là hàm chẵn nên nhận trục tung làm trục đối xứng)
|
Đồ thị hàm số $y=fleft( x right),,left( C right)$ |
Đồ thị hàm số $y=fleft( left| x right| right),,left( {{C}_{1}} right)$ |
|
|
|
Mẫu 3: Từ đồ thị hàm số $y=uleft( x right).vleft( x right),,left( C right)$ suy ra đồ thị hàm số $y=left| uleft( x right) right|.vleft( x right),,left( {{C}_{1}} right)$
Ta có: $y=left| uleft( x right) right|.vleft( x right),=left{ begin{align} & uleft( x right).vleft( x right),,text{khi u}left( x right)ge 0 \ & -uleft( x right).vleft( x right),,text{khi u}left( x right)<0 \ end{align} right.$. Do đó đồ thị hàm số $y=left| uleft( x right) right|.vleft( x right),,left( {{C}_{1}} right)$ gồm hai phần:
– Phần 1: Là phần của $left( C right)$ ứng với miền $text{u}left( x right)ge 0$.
– Phần 2: Lấy đối xứng phần của $left( C right)$ ứng với miền $text{u}left( x right)<0$ qua trục $Ox$.
Bài tập trắc nghiệm nhận dạng dạng đồ thị hàm số trị tuyệt đối có đáp án
|
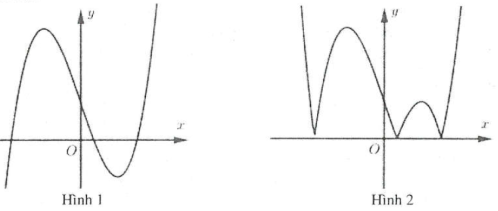
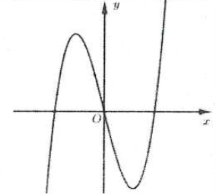
Ví dụ 1: Hình 1 là đồ thị hàm số $y={{x}^{3}}-3x+1$. Đồ thị hình 2 là đồ thị của hàm số nào trong các hàm số sau A. $y={{left| x right|}^{3}}-3left| x right|+1$. B. $y=left| {{x}^{3}}-3x+1 right|$. C. $y=left| {{left| x right|}^{3}}-3left| x right|+1 right|$. D. $y={{left| x right|}^{3}}-3x+1$. |
Lời giải
Đồ thị hình 2 gồm 2 phần:
– Phần 1: Là phần đồ thị của hình 1 nằm phía bên trên trục $Ox$.
– Phần 2: Lấy đối xứng phần đồ thị của hình 1 nằm dưới $Ox$ qua $Ox$.
Do đó đồ thị hình 2 là đồ thị hàm số $y=left| fleft( x right) right|=left| {{x}^{3}}-3x+1 right|$. Chọn B.
|
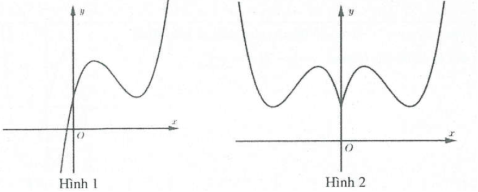
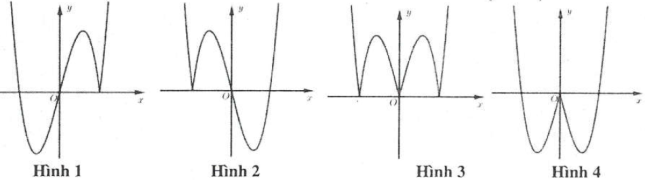
Ví dụ 2: Hình 1 là đồ thị hàm số $y={{x}^{3}}-4{{x}^{2}}+4x+1$. Đồ thị hình 2 là đồ thị của hàm số nào trong các hàm số sau A. $y=left| {{x}^{3}}-4{{x}^{2}}+4x+1 right|$. B. $y=left| {{left| x right|}^{3}}-4{{x}^{2}}+4left| x right|+1 right|$. C. $y=left| x right|x-4{{x}^{2}}+4left| x right|+1$. D. $y={{left| x right|}^{3}}+4{{x}^{2}}+4left| x right|+1$. |
Lời giải
Đồ thị hình 2 gồm 2 phần:
– Phần 1: Là phần đồ thị của hình 1 nằm bên phải trục $Oy$.
– Phần 2: Lấy đối xứng phần 1 qua $Oy$.
Do đó đồ thị hình 2 là đồ thị hàm số $y=left| fleft( x right) right|=left| x right|x-4{{x}^{2}}+4left| x right|+1$. Chọn C.
|
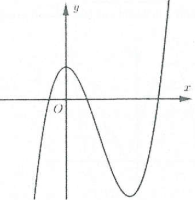
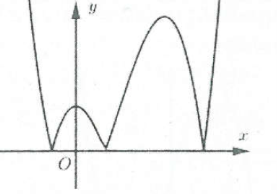
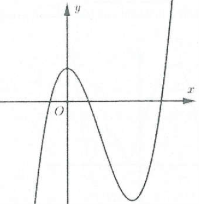
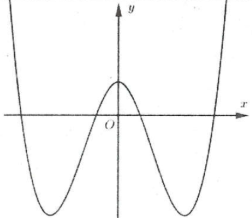
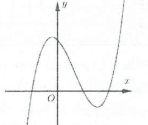
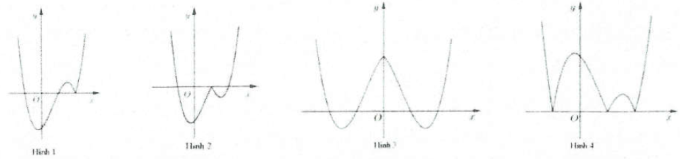
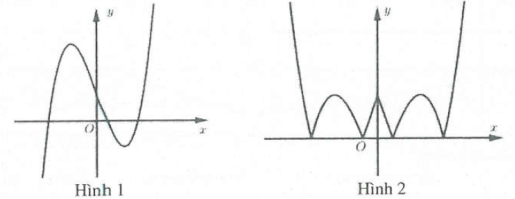
Ví dụ 3: [Đề thi tham khảo của Bộ GD&ĐT năm 2017] Hàm số $y=left( x-2 right)left( {{x}^{2}}-1 right)$ có đồ thị nào như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số $y=left| x-2 right|left( {{x}^{2}}-1 right)$?
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. |
Lời giải
Đồ thị hàm số $y=left( x-2 right)left( {{x}^{2}}-1 right)$ cắt trục hoành tại điểm $x=1,x=2$
Áp dụng quy tắc phá giá trị tuyệt đối $y=left| x-2 right|left( {{x}^{2}}-1 right)=left{ begin{align} & left( x-2 right)left( {{x}^{2}}-1 right)text{ khi }xge 2 \ & -left( x-2 right)left( {{x}^{2}}-1 right)text{ khi }x<2 \ end{align} right.$
Đồ thị hàm số $y=left| x-2 right|left( {{x}^{2}}-1 right)$ gồm 2 phần:
– Phần 1: Là phần của đồ thị hàm số $y=left( x-2 right)left( {{x}^{2}}-1 right)$ với miền $xge 2$.
– Phần 2: Lấy đối xứng phần của đồ thị hàm số $y=left( x-2 right)left( {{x}^{2}}-1 right)$ ứng với miền $x<2$ qua trục hoành. Từ đó suy ra đồ thị hàm số có dạng như hình 1. Chọn A.
|
Ví dụ 4: Hàm số $y={{x}^{3}}-4x$ có đồ thị nào như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số $y=left| x-2 right|left( {{x}^{2}}+2x right)$? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. |
Lời giải
Ta có: $y=left| x-2 right|left( {{x}^{2}}+2x right)=left{ begin{align} & {{x}^{3}}-4xtext{ khi }xge 2 \ & -left( {{x}^{3}}-4x right)text{ khi }x<2 \ end{align} right.$
Do đó đồ thị hàm số $y=left| x-2 right|left( {{x}^{2}}+2x right)$ gồm 2 phần:
– Phần 1: Là phần của đồ thị $left( C right):y={{x}^{3}}-4x$ ứng với $xge 2$.
– Phần 2: Lấy đối xứng phần của $left( C right):y={{x}^{3}}-4x$ ứng với miền $x<2$ qua $Ox$.
Suy ra đồ thị hàm số $y=left| x-2 right|left( {{x}^{2}}+2x right)$ là hình 1. Chọn A.
|
Ví dụ 5: Hình 1 là đồ thị hàm số $y={{x}^{3}}-3x+1$. Đồ thị hình 2 là đồ thị của hàm số nào trong các hàm số sau A. $y=left| {{x}^{3}} right|-3left| x right|+1$. B. $y=left| {{x}^{3}} right|+3left| x right|+1$. C. $y=left| left| {{x}^{3}} right|-3left| x right|+1 right|$. D. $y=left| left| {{x}^{3}} right|+3left| x right|+1 right|$. |
Lời giải
Từ đồ thị hàm số $y={{x}^{3}}-3x+1$ ta suy ra đồ thị hàm số $y=left| {{x}^{3}} right|-3left| x right|+1$ như hình vẽ sau
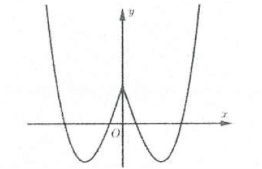
Đồ thị hình 2 gồm 2 phần:
Từ đó suy ra đồ thị hàm số ở hình 2 là đồ thị hàm số $y=left| left| {{x}^{3}} right|-3left| x right|+1 right|$. Chọn C.