BÀI TẬP THỰC TẾ ỨNG DỤNG MIN – MAX
Các bài toán thực tế về giá trị lớn nhất, giá trị nhỏ nhấtCác bài toán thực thế
| Bài tập 1: Người ta tiêm một loại thuốc vào mạch máu ở cánh tay phải của một bệnh nhân. Sau thời gian là t giờ, nồng độ thuốc hấp thu trong máu của bệnh nhân đó được xác định theo công thức $C(t)=frac{0,28t}{{{t}^{2}}+4}(0<t<24)$. Hỏi sau bao nhiêu giờ thì nồng độ thuốc hấp thu trong máu của bệnh nhân đó là cao nhất?
A. 24 giờ. B. 4 giờ. C. 2 giờ. D. 1 giờ. |
Lời giải chi tiết
Đáp án: Chọn C
Yêu cầu bài toán: Tìm giá trị của $tin (0;24)$ để $C(t)=frac{0,28t}{{{t}^{2}}+4}$ đạt giá trị lớn nhất
Xét hàm số $C(t)=frac{0,28t}{{{t}^{2}}+4}$trên $(0;24)$, có $C'(t)=frac{0,28({{t}^{2}}+4)-0,28t.2t}{{{({{t}^{2}}+4)}^{2}}}=frac{-0,28{{t}^{2}}+1,12}{{{({{t}^{2}}+4)}^{2}}}$
Phương trình $C'(t)=0Leftrightarrow left{ begin{array} {} 0<t<24 \ {} -0,28{{t}^{2}}+1,12=0 \ end{array} right.Leftrightarrow t=2.$ Tính $C(2)=0,07$
Suy ra $underset{(0;24)}{mathop{max }},C(t)=C(2)=0,07.$ Vậy sau 2 giờ thì nồng độ hấp thu là cao nhất.
| Bài tập 2: Người ta giới thiệu một loại thuốc kích thích sự sinh sản của một loại vi khuẩn. Sau ít phút, số vi khuẩn được xác định theo công thức $N(t)=1000+30{{t}^{2}}-{{t}^{3}},,(0le tle 30)$. Hỏi sau bao nhiêu phút thì số vi khuẩn lớn nhất?
A. 10 phút. B. 20 phút. C. 30 phút. D. 15 phút. |
Lời giải chi tiết
Đáp án: Chọn B
Yêu cầu bài toán: Tìm giá trị của $tin [0;30]$ để $N(t)=1000+30{{t}^{2}}-{{t}^{3}}$ đạt giá trị lớn nhất
Xét hàm số $N(t)=1000+30{{t}^{2}}-{{t}^{3}}$ trên [0;3], có $N'(t)=60t-3{{t}^{2}}$
Phương trình $N'(t)=0Leftrightarrow left{ begin{array} {} 0le tle 30 \ {} 60t-3{{t}^{2}}=0 \ end{array} right.Leftrightarrow t=20$. Tính $left{ begin{array} {} N(0)=N(30)=1000 \ {} N(20)=5000 \ end{array} right.$
Suy ra $underset{text{ }!![!!text{ }0;30]}{mathop{max }},N(t)=N(20)=5000.$ Vậy sau 20 phút thì số vi khuẩn là lớn nhất.
| Bài tập 3: Ông A muốn mua một mảnh đất hình chữ nhật có diện tích bằng 100m2 để làm khu vườn. Hỏi người đó phải mua mảnh đất có kích thước như thế nào để chi phí xây dựng bờ rào là ít tốn kém nhất?
A. 10m x 10m. B. 4m x 25m. C. 5m x 20m. D. 25m x 8m. |
Lời giải chi tiết
Đáp án: Chọn A
Yêu cầu bài toán: Cho diện tích và tìm giá trị nhỏ nhất của chu vi hình chữ nhật
Gọi x, y lần lượt là chiều rộng, chiều dài của hình chữ nhật
Diện tích hình chữ nhật là $S=xy=100Leftrightarrow y=frac{100}{x}$
Chu vi hình chữ nhật (bờ rào mảnh đất) là $C=2x+2y=2x+frac{200}{x}$
Áp dụng bất đẳng thức Cosi, ta có $2x+frac{200}{x}ge 2sqrt{2.frac{200}{x}}=40Rightarrow {{C}_{min }}=40$
Dấu bằng xảy ra khi và chỉ khi $2x=frac{200}{x}Leftrightarrow {{x}^{2}}=100Leftrightarrow x=10Rightarrow y=10$
| Bài tập 4: Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật có đáy là hình vuông sao cho thể tích khối hộp được tạo thành là 8dm3 và diện tích toàn phần đạt giá trị nhỏ nhất. Độ dài cạnh đáy của mỗi hộp muốn thiết kế là
A. $2sqrt[3]{2}dm.$ B. $2dm.$ C. $4dm.$ D. $2sqrt{2}dm.$ |
Lời giải chi tiết
Đáp án: Chọn B
Gọi h, x lần lượt là chiều cao và độ dài cạnh đáy của hình hợp chữ nhật
Thể tích khối hộp chữ nhật là $V=Bh={{x}^{2}}h=8Leftrightarrow h=frac{8}{{{x}^{2}}}$
Diện tích toàn phần hình hộp chữ nhật là ${{S}_{tp}}={{S}_{xq}}+{{S}_{d}}=4hx+2{{x}^{2}}=2{{x}^{2}}+frac{32}{x}$
Ta có $2{{x}^{2}}+frac{32}{x}=2{{x}^{2}}+frac{16}{x}+frac{16}{x}ge 3sqrt[3]{2{{x}^{2}}.frac{16}{x}.frac{16}{x}}=24Rightarrow {{S}_{min }}=24$
Dấu bằng xảy ra khi và chỉ khi $2{{x}^{2}}=frac{16}{x}Leftrightarrow {{x}^{3}}=8Leftrightarrow x=2$
| Bài tập 5: Cho một tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh x cm, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
A. $x=4.$ B. $x=3.$ C. $x=2.$ D. $x=1.$ |
Lời giải chi tiết
Đáp án: Chọn C
Khi cắt và gấp tấm nhôm, ta được hình hộp chữ nhật có chiều cao x; đáy là hình vuông cạnh
$12-2xRightarrow $ Thể tích khối hộp chữ nhật là $V=Bh=x.(12-2x)(12-2x)$
Cách 1. Khảo sát hàm số $f(x)=x.(12-2x).(12-2x)$ trên $(0;6)xrightarrow{{}}underset{(0;6)}{mathop{max }},f(x)$
Cách 2. Ta có $4x(12-2x).(12-2x)le frac{{{(4x+12-2x+12-2x)}^{3}}}{27}=512Rightarrow Vle 128$
Dấu bằng xảy ra khi và chỉ khi $4x=12-2xLeftrightarrow 6x=12Leftrightarrow x=2.$
| Bài tập 6: Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ hộp là ít nhất (diện tích toàn phần của lon là nhỏ nhất). Bán kính đáy vỏ lon là bao nhiêu khi ta muốn có thể tích lon là 314 cm3 ?
A. $R=sqrt[3]{frac{314}{pi }}.$ B. $R=sqrt[3]{frac{628}{pi }}.$ C. $R=942sqrt[3]{2pi }.$ D. $R=sqrt[3]{frac{314}{2pi }.}$ |
Lời giải chi tiết
Đáp án: Chọn D
Gọi R, h lần lượt là bán kính đáy, chiều cao của lon sữa
Thể tích của lon sữa hình trụ là $V=pi {{R}^{2}}h=314Leftrightarrow h=frac{314}{pi {{R}^{2}}}$
Diện tích nguyên liệu làm vỏ hộp (${{S}_{tp}}$ hình trụ) là ${{S}_{tp}}=2pi Rh+2pi {{R}^{2}}=2pi {{R}^{2}}+frac{628}{R}$
Ta có $2pi {{R}^{2}}+frac{628}{R}=2pi {{R}^{2}}+frac{314}{R}+frac{314}{R}ge 3sqrt[3]{2pi {{R}^{2}}.frac{314}{R}.frac{314}{R}}=3sqrt[3]{2.{{(314)}^{2}}pi }$
Dấu bằng xảy ra khi $2pi {{R}^{2}}=frac{314}{R}Leftrightarrow {{R}^{3}}=frac{314}{2pi }Leftrightarrow R=sqrt[3]{frac{314}{2pi }}$
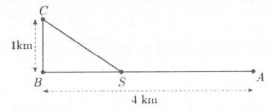
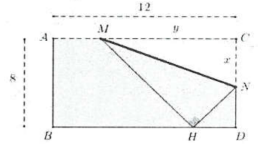
| Bài tập 7: Một đường dây điện được nối từ nhà máy điện trên đất liền ở vị trí A đến vị trí C một hòn đảo. Khoảng cách ngắn nhất từ C đến đất liền là $BC=1km$, khoảng cách từ A đến B là 4 km. Người ta chọn một vị trí điểm S nằm giữa A và B để mắc đường dây điện đi từ A đến S, rồi từ S đến C như hình vẽ dưới đây. Chi phí mỗi km dây điện trên đất liền là 3000 USD, mỗi km trên điện đặt ngầm dưới biển mất 5000 USD, Hỏi điểm S phải cách A bao nhiên km để chi phí mắc đường dây điện ít nhất?
A. $frac{5}{2}km.$ B. 2 km. C. $frac{13}{4}km.$ D. $frac{7}{2}km$ |
Lời giải chi tiết
Đáp án: Chọn C
Đặt $SA=x,(km;,,0le xle 4),$ ta có $SA+SB=ABRightarrow SB=4-x,(km)$
Tam giác SBC vuông tại B, có $SC=sqrt{S{{B}^{2}}+B{{C}^{2}}}=sqrt{1+{{(4-x)}^{2}}}=sqrt{{{x}^{2}}-8x+17}$
Do đó, số tiền để mắc dây điện trên đất liền là ${{T}_{1}}=$3000 x SA = 3000x
Số tiền để mắc dây điện ngầm dưới biển là ${{T}_{2}}=5000,$x $SC=5000sqrt{{{x}^{2}}-8x+17}$
Suy ra tổng số tiền mắc dây điện là $T={{T}_{1}}+{{T}_{2}}=3000x+5000sqrt{{{x}^{2}}-8x+17}$
Xét hàm số $f(x)=3x+5sqrt{{{x}^{2}}-8x+17}$ trên [0;4], có $f'(x)=3+frac{5x-20}{sqrt{{{x}^{2}}-8x+17}}$
Phương trình $f'(x)=0Leftrightarrow 3sqrt{{{x}^{2}}-8x+17}=20-5xLeftrightarrow x=frac{13}{4}$
Dựa vào bảng biến thiên, ta được $underset{text{ }!![!!text{ }0;4]}{mathop{min }},f(x)=fleft( frac{13}{4} right)=16$
Vậy số tiền ít nhất là $T=100.16=16000,USD.$ Dấu bằng xảy ra khi $x=frac{13}{4}$
| Bài tập 8: Một sợi dây kim loại dài 60 cm được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh a, đoạn dây thứ hai uốn thành đường tròn bán kính r. Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì tỉ số $frac{a}{r}$ bằng
A. 1. B. 2. C. 3. D. 4. |
Lời giải chi tiết
Đáp án: Chọn B
Gọi x là độ dài của đoạn dây cuộn thành hình tròn $(0<x0$
Suy ra hàm S chỉ có một cực trị và là cực tiểu tại $x=frac{60pi }{4+pi }$
Do đó S đạt giá trị nhỏ nhất tại $x=frac{60pi }{4+pi }$
Với $x=frac{60pi }{4+pi }xrightarrow{{}}r=frac{30}{(4+pi )}$ và $a=frac{240}{(4+pi ).4}xrightarrow{{}}frac{a}{r}=frac{240}{120}=2$
| Bài tập 9: Doanh nghiệp Alibaba cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai máy A và B. Máy A làm việc trong x ngày và cho số tiền lãi là ${{x}^{3}}+2x$ (triệu đồng), máy B làm việc trong y ngày và cho số tiền lãi là $326y-27{{y}^{2}}$ (triệu đồng). Hỏi doanh nghiệp Alibaba cần sử dụng máy A làm việc trong bao nhiêu ngày sao cho số tiền lãi là nhiều nhất? (Biết rằng A và B không đồng thời làm việc, máy B làm việc không quá 6 ngày).
A. 5. B. 6. C. 7. D. 4. |
Lời giải chi tiết
Đáp án: Chọn B
Tổng số tiền hai máy làm được là $T={{T}_{A}}+{{T}_{B}}={{x}^{3}}-27{{y}^{2}}+2x+326y$
Theo bài ra, ta có $x+y=10;yle 6$ nên $y=10-x$ và $4le xle 10$
Suy ra $T={{x}^{3}}-27{{(10-x)}^{2}}+2x+326(10-x)={{x}^{3}}-27{{x}^{2}}+216x+560$
Xét hàm số $f(x)={{x}^{3}}-27{{x}^{2}}+216x+560$ trên [4;10], có $f'(x)=3({{x}^{2}}-18x+72)$
Phương trình $f'(x)=0Leftrightarrow x=6xrightarrow{{}}underset{text{ }!![!!text{ }4;10]}{mathop{max }},f(x)=f(6)=1100$
Vậy $x=6$ thỏa mãn yêu cầu bài toán.
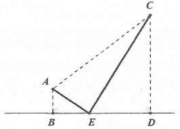
| Bài tập 10: Có hai cây cột dựng đứng trên mặt đất lần lượt là $AB=1m,,,,CD=4m$ và đỉnh của hai cột là hai điểm A và C cách nhau 5m. Người ta chọn một vị trí trên mặt đất (nằm giữa B, D) để giăng dây nối đến hai đỉnh cột để trang trí như mô hình bên. Tính độ dài ngắn nhất của đoạn dây?
A. $sqrt{41}.$ B. $sqrt{37}.$ C. $sqrt{29}.$ D. $3sqrt{5}.$ |
Lời giải chi tiết
Đáp án: Chọn A
- Cách 1: Đặt $BE=x$ với $x>0$. Ta có $BD=sqrt{{{5}^{2}}-{{(4-1)}^{2}}}=4$ nên $ED=BD-BE=4-x$
Lại có $AE+EC=sqrt{{{x}^{2}}+1}+sqrt{{{(4-x)}^{2}}+16}$. Đặt $f(x)=sqrt{{{x}^{2}}+1}+sqrt{{{x}^{2}}-8x+32},x>0$
Ta có $f'(x)=frac{x}{sqrt{{{x}^{2}}+1}}+frac{x-4}{sqrt{{{x}^{2}}-8x+32}};forall x>0$
Giải phương trình $f'(x)=0,$ ta thu được $x=frac{4}{5}$ và tìm được $min f(x)=sqrt{41}$
- Cách 2: Gọi H là điểm đối xứng với A qua B và K là điểm đối xứng với C qua D
Và I là hình chiếu của A lên CD. Khi đó AHKC là hình thang cân và $AG=sqrt{A{{C}^{2}}-G{{C}^{2}}}=4$
Ta thấy $EC=EK$ nên $AE+EC=AE+EK$
Để ${{left{ AE+EC right}}_{min }}$ khi và chỉ khi ${{left{ AE+EK right}}_{min }}$ và điều đó có nghĩa là A, E, K thẳng hàng.
Vì thế $AK=sqrt{K{{G}^{2}}+A{{G}^{2}}}=sqrt{{{4}^{2}}+{{5}^{2}}}=sqrt{41}$. Hay độ dài ngắn nhất của đoạn dây chính bằng $sqrt{41}$
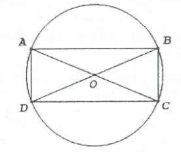
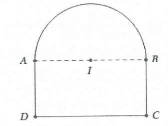
| Bài tập 11: Một mảnh vườn hình chữ nhật có diện tích 961 m2, người ta muốn mở rộng thêm 4 phần đất sao cho tạo thành hình tròn ngoại tiếp mảnh vườn. Biết tâm hình tròn trùng với tâm của hình chữ nhật (xem hình minh họa). Tính diện tích nhỏ nhất ${{S}_{min }}$ của 4 phần đất được mở rộng
A. ${{S}_{min }}=961pi -961.$ B. ${{S}_{min }}=1922pi -961.$ C. ${{S}_{min }}=1892pi -946.$ D. ${{S}_{min }}=480,5pi -961.$ |
Lời giải chi tiết
Đáp án: Chọn D
Gọi x (m), y (m) (x>0, y>0) lần lượt là hai kích thước mảnh vườn hình chữ nhật;
R (m) là bán kính hình tròn ngoại tiếp mảnh vườn $xrightarrow{{}}{{R}^{2}}=O{{B}^{2}}=frac{{{x}^{2}}+{{y}^{2}}}{4}$
Theo đề bài, ta có $xy=961,,{{m}^{2}}$. Diện tích 4 phần đất mở rộng: $S={{S}_{tron}}-{{S}_{ABCD}}=pi {{R}^{2}}-xy$
$=pi .frac{({{x}^{2}}+{{y}^{2}})}{4}-xyoverset{Cosi}{mathop{ge }},pi .frac{2xy}{4}-xy=480,5pi -961$
| Bài tập 12: Cho một tờ giấy hình chữ nhật với chiều dài 12cm và chiều rộng 8cm. Gấp góc bên phải của tờ giấy sao cho sau khi gấp, đỉnh của góc đó chạm đáy dưới như hình vẽ. Để độ dài nếp gấp là nhỏ nhất thì giá trị nhỏ nhất đó bằng bao nhiêu?
A. 6. B. $6sqrt{5}.$ C. $6sqrt{2}.$ D. $6sqrt{3}.$ |
Lời giải chi tiết
Đáp án: Chọn D
Đặt $CN=x(cm)$ và $MC=y,(cm)$
Độ dài đường gấp khúc cần tìm chính là độ dài đoạn thẳng $MN=sqrt{{{x}^{2}}+{{y}^{2}}}$
Dễ thấy MHNC là hình thoi nên $MC=MH=y,,NC=NH=x$
Gọi K là hình chiếu của M xuống $BDRightarrow MK=8Rightarrow HK=sqrt{{{y}^{2}}-64}$
Mà $HD=sqrt{H{{N}^{2}}-N{{D}^{2}}}=sqrt{{{x}^{2}}-{{(8-x)}^{2}}}=sqrt{16x-64}=4sqrt{x-4}$
$Rightarrow KD=y=HK+HD=sqrt{{{y}^{2}}-64}+4sqrt{x-4}Leftrightarrow y-sqrt{{{y}^{2}}-64}=4sqrt{x-4}$
$Leftrightarrow frac{64}{y+sqrt{{{y}^{2}}-64}}=4sqrt{x-4}Leftrightarrow y+sqrt{{{y}^{2}}-64}=frac{16}{sqrt{x-4}}$
Khi đó $2y=frac{16}{sqrt{x-4}}+4sqrt{x-4}Leftrightarrow y=frac{8+2(x-4)}{sqrt{x-4}}=frac{2x}{sqrt{x-4}}$
Do đó $M{{N}^{2}}={{x}^{2}}+{{y}^{2}}={{x}^{2}}+frac{4{{x}^{2}}}{x-4}.$ Đặt $f(x)={{x}^{2}}+frac{4{{x}^{2}}}{x-4}$ với $8>x>4$
Có $f'(x)=2x+4-frac{64}{{{(x-4)}^{2}}};f'(x)=0Leftrightarrow (x+2){{(x-4)}^{2}}=32Leftrightarrow x=6$
Suy ra $underset{(4;8)}{mathop{min }},f(x)=f(6)=108Rightarrow MN_{min }^{2}=108Rightarrow M{{N}_{min }}=6sqrt{3}$
| Bài tập 13: Một cửa sổ có hình dạng như hình bên, bao gồm: một hình chữ nhật ghép với nửa hình tròn có tâm nằm trên cạnh của hình chữ nhật. Biết rằng tổng độ dài đường viền cho phép của cửa sổ là 4m. Hỏi diện tích lớn nhất của cửa sổ là bao nhiêu?
A. $S=frac{4}{4+pi }.$ B. $S=frac{8}{4+pi }.$ C. $S=frac{4}{8+pi }.$ D. $S=frac{8}{8+pi }.$ |
Lời giải chi tiết
Đáp án: Chọn B
Gọi $left{ begin{array} {} AD=BC=x \ {} AI=IB=R \ end{array} right.Rightarrow {{C}_{hcn}}=CD+2BC=2(R+x);{{C}_{hcn}}=pi R$
Suy ra $pi R+2(R+x)=4Leftrightarrow x=frac{4-(pi +2)R}{2}$
Và ${{S}_{hcn}}=AB.BC=2Rx;{{S}_{hcn}}=frac{pi {{R}^{2}}}{2}$
Tổng diện tích của cửa sổ là
$S=2Rx+frac{pi {{R}^{2}}}{2}=2R.frac{4-(pi +2)R}{2}+frac{pi {{R}^{2}}}{2}=Rleft[ 4-(pi +2)R right]+frac{pi {{R}^{2}}}{2}$
$=4R-left( 2+frac{pi }{2} right){{R}^{2}}=frac{8}{4+pi }-{{left( sqrt{frac{8}{4+pi }}-Rsqrt{2+frac{pi }{2}} right)}^{2}}le frac{8}{4+pi }$
Do đó diện tích lớn nhất của cửa sổ là $S=frac{8}{4+pi }$
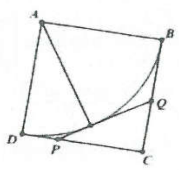
| Bài tập 14: Cho hình vuông ABCD độ dài cạnh bằng 2m như hình vẽ. Lấy hai điểm P, Q (thay đổi) lần lượt nằm trên hai cạnh DC, CB sao cho PQ luôn tiếp xúc với đường tròn tâm A bán kính AB. Tìm giá trị nhỏ nhất độ dài đoạn thẳng PQ (kết quả làm tròn đến hàng phần trăm)
A. 1,08 m. B. 1,32 m. C. 1,66 m. D. 1,54 m. |
Lời giải chi tiết
Đáp án: Chọn C
Đặt $widehat{DAP}=x$, ta có $widehat{DAP}+widehat{BAQ}=frac{1}{2}widehat{A}={{45}^{o}}$ suy ra $widehat{BAQ}={{45}^{o}}-x$
Khi đó $PQ=ADtan ,x+ABtan ({{45}^{o}}-x)=2left( tan ,x+frac{1-tan ,x}{1+tan ,x} right)=2.frac{{{tan }^{2}},x+1}{tan ,x+1}$
Đặt $t=tan ,x,(0<t<1),$ ta được $PQ=frac{2{{t}^{2}}+2}{t+1}$
Xét $f(t)=frac{{{t}^{2}}+1}{t+1}$ trên (0;1), có $f'(t)=frac{{{t}^{2}}+2t-1}{{{(t+1)}^{2}}};f'(t)=0Leftrightarrow t=-1+sqrt{2}$
Suy ra hàm số $f(t)$ đạt giá trị nhỏ nhất khi $t=-1+sqrt{2}.$ Vậy $P{{Q}_{min }}approx 1,66.$