Biện luận số nghiệm của phương trình bằng đồ thị kết hợp với đặt ẩn phụ
Bài toán: Cho hàm số $y=fleft( x right)$. Biện luận số nghiệm của phương trình $fleft[ uleft( x right) right]=m$.
Phương pháp giải bài toán biện luận số nghiệm của phương trình
§ Bước 1: Đặt $t=uleft( x right)$ ta cần xác định miền giá trị của $t$ và tương ứng với mỗi giá trị của $t$ có bao nhiêu giá trị của $x$.
(Ta có thể lập bảng biến thiên hàm số $t=uleft( x right)$ để nhận xét và tìm miền của $t$).
§ Bước 2: Dựa vào đồ thị, biện luận số nghiệm của phương trình $fleft( t right)=m$ từ đó suy ra số nghiệm của phương trình $fleft[ uleft( x right) right]=m$.
Bài tập vận dụng khó về biện luận số nghiệm của phương trình có đáp án
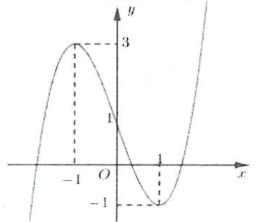
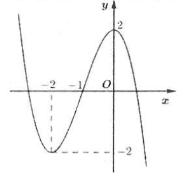
| Bài tập 1: [Đề thi tham khảo năm 2018] Cho hàm số $y=fleft( x right)$ liên tục trên $mathbb{R}$ và có đồ thị như hình vẽ bên
Tập hợp tất cả các giá trị thực của tham số $m$ để phương trình $fleft( sin x right)=m$ có nghiệm thuộc khoảng $left( 0;pi right)$ là A. $left[ -1;3 right)$ B. $left( -1;1 right)$ C. $left( -1;3 right)$ D. $left[ -1;1 right)$ |
Lời giải chi tiết
Đặt $t=sin x$, với $xin left( 0;pi right)Rightarrow tin left( 0;1 right]$. Khi đó $fleft( sin x right)=mLeftrightarrow fleft( t right)=m$.
Dựa vào đồ thị hàm số, để $fleft( t right)=m$ có nghiệm thuộc $left( 0;1 right]$ $Leftrightarrow -1le m<1$. Chọn D.
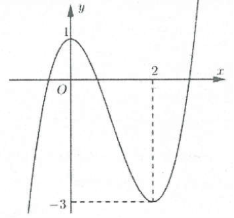
| Bài tập 2: Cho hàm số $y=fleft( x right)={{x}^{3}}-3{{x}^{2}}+1$ liên tục trên $mathbb{R}$và có đồ thị như hình vẽ bên.
Số các giá trị nguyên của tham số $m$ để phương trình $fleft( sqrt{x}+sqrt{1-x} right)=m$ có nghiệm thuộc đoạn $left[ 0;1 right]$ là: A. 2 B. 3 C. 4 D. 5 |
Lời giải chi tiết
Đặt $t=sqrt{x}+sqrt{1-x}Rightarrow {{t}^{2}}+2sqrt{xleft( 1-x right)}left( t>0 right)$
Theo bất đẳng thức Cosi ta có: $sqrt{xleft( 1-x right)}le frac{x+1-x}{2}=frac{1}{2}$
Do đó $1le {{t}^{2}}le 2Rightarrow 1le tle sqrt{2}$. Vậy $xin left[ 0;1 right]Rightarrow tin left[ 1;sqrt{2} right]$
Ta có: $fleft( 1 right)=-1,,,fleft( sqrt{2} right)=2sqrt{2}-5$
Kết hợp đồ thị suy ra phương trình $fleft( t right)=m$ có nghiệm thuộc đoạn $left[ 1;sqrt{2} right]$ thì $min left[ 2sqrt{2}-5;-1 right]$
Vậy có 2 giá trị nguyên của $min left{ -2;-1 right}$ để phương trình đã cho có nghiệm. Chọn A.
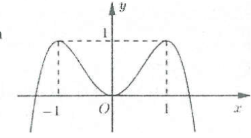
| Bài tập 3: Cho hàm số $y=fleft( x right)=-{{x}^{4}}+2{{x}^{2}}$ liên tục trên $mathbb{R}$ và có đồ thị như hình vẽ bên.
Số các giá trị nguyên của tham số $m$ để phương trình $-{{left( 1-sin x right)}^{4}}+2{{left( 1-sin x right)}^{2}}=m$ có nghiệm là: A. 2 B. 8 C. 3 D. 9 |
Lời giải chi tiết
Đặt $t=1-sin x$ ta có: $sin xin left[ -1;1 right]Rightarrow tin left[ 0;2 right]$
Ta có: $fleft( 2 right)=-8$. Dựa vào đồ thị hàm số ta thấy $tin left[ 0;2 right]Rightarrow fleft( t right)in left[ -8;1 right]$
Vậy phương trình $-{{left( 1-sin x right)}^{4}}+2{{left( 1-sin x right)}^{2}}=m$ có nghiệm khi $min left[ -8;1 right]$
Kết hợp $min mathbb{Z}Rightarrow $ có 9 giá trị của $m$. Chọn D.
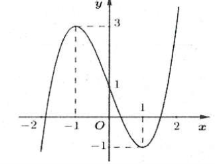
| Bài tập 4: Cho hàm số $y=fleft( x right)$ có đồ thị như hình vẽ bên.
Số nghiệm của phương trình $fleft[ fleft( x right) right]=0$ là: A. 6 B. 7 C. 8 D. 9 |
Lời giải chi tiết
Đặt $t=fleft( x right)Rightarrow fleft( t right)=0Leftrightarrow left[ begin{array} {} t=fleft( x right)=a \ {} t=fleft( x right)=b \ {} t=fleft( x right)=c \ end{array} right.$ dựa vào đồ thị ta có: $ain left( -2;-1 right),,,bin left( 0;1 right),,,cin left( 1;2 right)$
Khi đó dựa vào đồ thị ta lại có phương trình $fleft( x right)=a$ có 1 nghiệm, phương trình $fleft( x right)=b$ và phương trình $fleft( x right)=c$ đều có 3 nghiệm.
Do đó phương trình $fleft[ fleft( x right) right]=0$ có 7 nghiệm. Chọn B.
| Bài tập 5: Cho hàm số $y=fleft( x right)$ có đạo hàm trên $mathbb{R}$ và có đồ thị là đường cong như hình vẽ.
Đặt $gleft( x right)=fleft[ fleft( x right) right]$. Số nghiệm của phương trình ${g}’left( x right)=0$ là: A. 6 B. 7 C. 8 D. 9 |
Lời giải chi tiết
Ta có: ${g}’left( x right)={f}’left( x right).{f}’left[ fleft( x right) right]=0Leftrightarrow left[ begin{array} {} {f}’left( x right)=0 \ {} {f}’left[ fleft( x right) right]=0 \ end{array} right.$
Dựa vào đồ thị hàm số ta thấy ${f}’left( x right)=0Leftrightarrow left[ begin{array} {} x=-2 \ {} x=0 \ end{array} right.Rightarrow {f}’left( x right)=0$ có 2 nghiệm phân biệt $x=-2,,,x=0$.
Lại có: ${f}’left[ fleft( x right) right]=0Leftrightarrow left[ begin{array} {} fleft( x right)=-2 \ {} fleft( x right)=0 \ end{array} right.$
Phương trình $fleft( x right)=-2$ có 2 nghiệm $x=-2,,,x>0$ (nghiệm $x=-2$ bị lặp).
Phương trình $fleft( x right)=0$ có 3 nghiệm phân biệt.
Do đó phương trình ${g}’left( x right)=0$ có 6 nghiệm phân biệt. Chọn A.
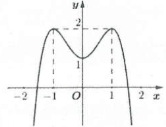
| Bài tập 6: Cho hàm số $y=fleft( x right)=-{{x}^{4}}+2{{x}^{2}}+1$ có đồ thị như hình vẽ bên.
Số giá trị nguyên của $m$ để phương trình $fleft[ fleft( x right) right]=m$ có nghiệm $xin left[ -1;1 right]$. A. 10 B. 11 C. 12 D. 13 |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy với $xin left[ -1;1 right]Rightarrow fleft( x right)in left[ 1;2 right]$
Đặt $t=fleft( x right)$, xét phương trình $fleft( t right)=m$ với $tin left[ 1;2 right]$
Dựa vào đồ thị hàm số với $tin left[ 1;2 right]Rightarrow fleft( t right)in left[ -7;2 right]$
Do đó phương trình $fleft[ fleft( x right) right]=m$ có nghiệm $xin left[ -1;1 right]Leftrightarrow min left[ -7;2 right]$
Kết hợp $min mathbb{Z}Rightarrow $ có 10 giá trị của $m$. Chọn A.
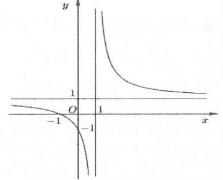
| Bài tập 7: Cho hàm số $y=frac{x+1}{x-1}$ có đồ thị như hình vẽ.
Tìm $m$ để phương trình $frac{sin x+1}{sin x-1}=m$ có nghiệm $xin left[ -frac{pi }{2};0 right)$ A. $min left[ -1;0 right]$ B. $min left[ -1;0 right)$ C. $min left[ -1;+infty right)$ D. $min left( -1;0 right]$ |
Lời giải chi tiết
Ta có: $xin left[ -frac{pi }{2};0 right)Rightarrow sin xin left[ -1;0 right)$. Đặt $t=sin xRightarrow frac{t+1}{t-1}=m$ với $tin left[ -1;0 right)$
Dựa vào đồ thị hàm số ta thấy phương trình $fleft( t right)=m$ có nghiệm $tin left[ -1;0 right)Leftrightarrow min left( -1;0 right]$. Chọn D.
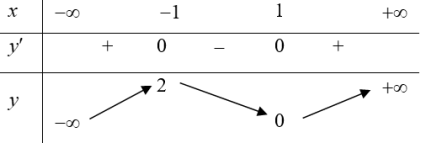
| Bài tập 8: Cho hàm số $y=fleft( x right)$ có đạo hàm trên $mathbb{R}$ và có bảng biến thiên như hình vẽ dưới đây
Số nghiệm của phương trình ${f}’left[ fleft( x right) right]=0$ là: A. 4 B. 7 C. 6 D. 3 |
Lời giải chi tiết
Đặt $gleft( x right)=fleft[ fleft( x right) right]$ ta có: ${g}’left( x right)={f}’left( x right).{f}’left[ fleft( x right) right]=0Leftrightarrow left[ begin{array} {} {f}’left( x right)=0 \ {} {f}’left[ fleft( x right) right]=0 \ end{array} right.$
Dựa vào đồ thị hàm số ta thấy ${f}’left( x right)=0Leftrightarrow left[ begin{array} {} x=-1 \ {} x=1 \ end{array} right.Rightarrow {f}’left( x right)=0$ có 2 nghiệm phân biệt $x=pm 1$.
Lại có: ${f}’left[ fleft( x right) right]=0Leftrightarrow left[ begin{array} {} fleft( x right)=-1 \ {} fleft( x right)=1 \ end{array} right.$Phương trình $fleft( x right)=-1$ có một nghiệm duy nhất
Phương trình $fleft( x right)=1$ có 3 nghiệm phân biệt.
Do đó phương trình ${g}’left( x right)=0$ có 6 nghiệm phân biệt. Chọn C.