CÁCH NHẬN DẠNG ĐỒ THỊ HÀM SỐ BẬC 4 TRÙNG PHƯƠNG: $y=a{{x}^{4}}+b{{x}^{2}}+c$ $left( ane 0 right)$
1. Giới hạn, đạo hàm và cực trị hàm bậc 4
Giới hạn
– Với $a>0$ thì $underset{xto pm infty }{mathop{lim }},y=+infty $.
– Với $a<0$ thì $underset{xto pm infty }{mathop{lim }},y=-infty $.
Đạo hàm và cực trị: ${y}’=4a{{x}^{2}}+2bx=2xleft( 2a{{x}^{2}}+b right)$ nên ${y}’=0Leftrightarrow left[ begin{array} {} x=0 \ {} {{x}^{2}}=-frac{b}{2a} \ end{array} right.$
– Với $abge 0$ thì hàm số có một điểm cực trị $x=0$.
– Với $ab<0$ thì hàm số có 3 điểm cực trị $x=0,,,x=pm sqrt{frac{-b}{2a}}$
2. Bảng biến thiên hàm trùng phương
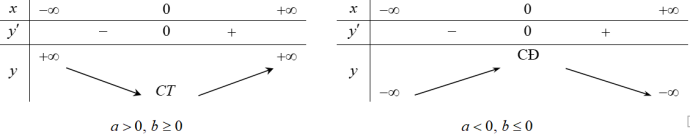
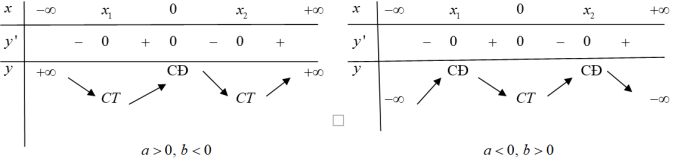 3. Đồ thị hàm số bậc 4
3. Đồ thị hàm số bậc 4
|
|
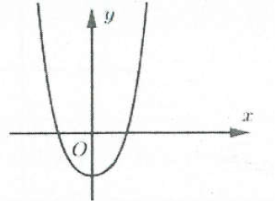
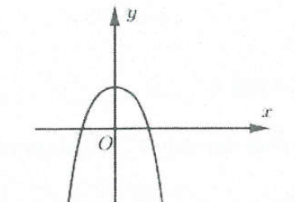
$abge 0$ |
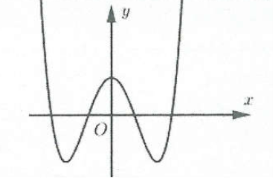
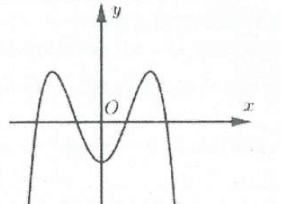
$ab<0$ |
|
$a>0$ |
|
|
|
$a<0$ |
|
|
Đồ thị hàm số nhận trục tung làm trục đối xứng.
4. Phương pháp giải toán
Để nhận diện đồ thị hàm số bậc 4 trùng phương: $y=a{{x}^{4}}+b{{x}^{2}}+c$ $left( ane 0 right)$ ta làm như sau:
Dựa vào $underset{xto +infty }{mathop{lim }},y$ để xác định hệ số $a$:
Dựa vào giao điểm với trục tung $left( 0;d right)$ suy ra tính chất của hệ số $d$
Dựa vào số điểm cực trị của đồ thị hàm số và hệ số a để xác định hệ số b.
– Với $abge 0$ thì hàm số có một cực trị.
– Với $ab<0$ thì hàm số có 3 cực trị.