Tính nhanh Góc giữa hai mặt bên có đáp án chi tiết
Phương pháp xác định góc giữa hai mặt bên:
Tính góc giữa hai mặt bên (SAC) và (SBC).
þ Cách 1: Tính góc giữa 2 đường thẳng a và b lần lượt vuông góc với mặt phẳng (SAC) và (SBC).
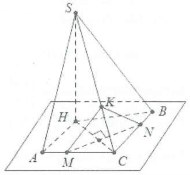
þ Cách 2: Dựng đường cao $SHbot left( ABC right).$
Lấy điểm M bất kỳ thuộc AC, dựng $MNbot HC.$
Lại có: $MNbot SHRightarrow MNbot left( SHC right)Rightarrow MNbot SC.$
Dựng $MKbot SCRightarrow SCbot left( MKN right)$
$Rightarrow widehat{left( left( SAC right);left( SBC right) right)}=widehat{left( MK,KN right)}.$
Bài tập tính nhanh góc giữa hai mặt bên có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B có $AB=a,BC=asqrt{3}$. Biết $SA=frac{asqrt{6}}{2}$, tính góc giữa hai mặt phẳng (SAC) và (SBC). |
Lời giải chi tiết
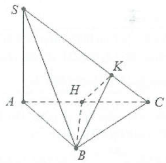
Dựng $BHbot ACRightarrow BHbot left( SAC right)Rightarrow BHbot SC.$
Dựng $BHbot SCRightarrow left( HKB right)bot SC$
$Rightarrow widehat{left( left( SBC right);left( SAC right) right)}=widehat{HKB}.$
Ta có: $SA=sqrt{S{{B}^{2}}-A{{B}^{2}}}=frac{asqrt{2}}{2};AC=sqrt{A{{B}^{2}}-B{{C}^{2}}}=2a.$
Khi đó $sin widehat{KCH}=frac{HK}{HC}=frac{SA}{SC}=frac{SA}{sqrt{S{{A}^{2}}+A{{C}^{2}}}}=frac{1}{3}Rightarrow HK=frac{a}{3}.$
Mặt khác: $BH=frac{BA.BC}{AC}=frac{asqrt{3}}{2}Rightarrow tan widehat{HKB}=frac{BH}{HK}=sqrt{3}$
$Rightarrow widehat{HKB}=60{}^circ .$ Vậy góc giữa hai mặt phẳng (SAC) và (SBC) bằng $60{}^circ $.
| Bài tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a có $widehat{ABC}=60{}^circ $, $SAbot left( ABC right)$ và $SA=a$. Tính cosin góc giữa:
a) (SBC) và (SCD). b) (SBC) và (SCD). |
Lời giải chi tiết
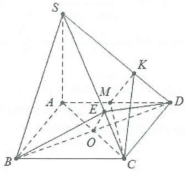
a) Nhận xét $Delta ABC$ là tam giác đều cạnh a vì $AB=BC=a$ và $widehat{ABC}=60{}^circ $. Gọi O là tâm của hình thoi ABCD.
Ta có: $left{ begin{array} {} BDbot AC \ {} BDbot SA \ end{array} right.Rightarrow BDbot left( SAC right)Rightarrow BDbot SC.$
Dựng $BEbot SCRightarrow SCbot left( BED right).$
Mặt khác: $SA=AC=aRightarrow Delta SAC$ vuông cân tại A suy ra
$widehat{ECO}=45{}^circ $. Khi đó $OE=OCsin 45{}^circ =frac{asqrt{2}}{4}.$
Lại có: $OB=frac{asqrt{3}}{2}Rightarrow tan widehat{BEO}=frac{OB}{OE}=sqrt{6}.$
Do $widehat{BED}=2widehat{BEO}$ sử dụng công thức lượng giác hoặc máy tính CASIO ta tính được $cos widehat{BED}=frac{-5}{7}$.
Cách khác: Ta có: $BE=DE=sqrt{O{{E}^{2}}+O{{B}^{2}}}=frac{sqrt{14}}{4}Rightarrow cos widehat{BED}=frac{E{{B}^{2}}+E{{D}^{2}}-B{{D}^{2}}}{2.EB.ED}=frac{-5}{7}.$
Suy ra $widehat{left( left( SBC right);left( SCD right) right)}=frac{5}{7}.$
b) Dựng $CMbot AD$ ta có: $left{ begin{array} {} CMbot AD \ {} CMbot SA \ end{array} right.Rightarrow CMbot left( SAD right)Rightarrow CMbot SD.$
Dựng $CKbot SDRightarrow SDbot left( MKC right).$
Tam giác ACD đều cạnh a nên $CM=frac{asqrt{3}}{2}$. Do $SA=AD=aRightarrow Delta SAD$ vuông cân tại A suy ra $widehat{SDM}=45{}^circ $. Do đó $MK=MDsin 45{}^circ =frac{asqrt{2}}{4}.$
Suy ra $tan widehat{MKC}=frac{CM}{MK}=sqrt{6}Rightarrow cos widehat{MKC}=frac{1}{sqrt{7}}.$
Vậy $cos widehat{left( left( SCD right);left( SAD right) right)}=frac{1}{sqrt{7}}.$
| Bài tập 3: Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều cạnh a với $AD=2a$, biết rằng $SAbot left( ABCD right)$ và mặt phẳng (SCD) tạo với đáy một góc $45{}^circ $. Tính cosin góc giữa 2 mặt phẳng (SCD) và (SBC). |
Lời giải chi tiết
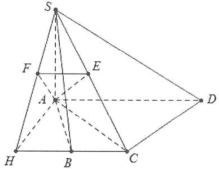
Do $AD=2a$ nên tứ giác ABCD nội tiếp trong đường tròn đường kính $AD=2a$
Ta có: $left{ begin{array} {} ACbot CD \ {} CDbot SA \ end{array} right.Rightarrow CDbot left( SAC right)$
Suy ra $widehat{left( left( SCD right);left( ABCD right) right)}=widehat{SCA}=45{}^circ $
$Rightarrow SA=AC=sqrt{4{{a}^{2}}-{{a}^{2}}}=asqrt{3}$
Dựng $AEbot SCRightarrow AEbot left( SCD right)$
Dựng $left{ begin{array} {} AHbot BC \ {} AFbot SH \ end{array} right.Rightarrow AFbot left( SBC right)$, góc giữa 2 mặt phẳng (SCD) và (SBC) là góc giữa AE và AF.
Tacó: $AE=frac{SA.AC}{sqrt{S{{A}^{2}}+A{{C}^{2}}}}=frac{asqrt{6}}{2}$; $AH=ACsin 30{}^circ =frac{asqrt{3}}{2}.$
Suy ra $AF=frac{SA.AH}{sqrt{S{{A}^{2}}+A{{H}^{2}}}}=frac{asqrt{3}}{sqrt{5}}$, do $AFbot left( SBC right)Rightarrow AFbot FE$. Do đó $cos widehat{FAE}=frac{AF}{AE}=frac{sqrt{10}}{5}.$
| Bài tập 4: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với $AB=a;AD=asqrt{3}$, cạnh bên $SAbot left( ABCD right)$. Biết mặt phẳng (SBC) tạo với mặt đáy một góc $60{}^circ $. Tính cosin góc giữa hai mặt phẳng (SBC) và (SCD). |
Lời giải chi tiết
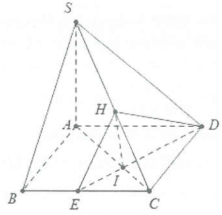
Do $SAbot left( ABCD right)$ và $BCbot ABRightarrow BCbot left( SBA right)$
Do đó $widehat{left( left( SBC right);left( ABC right) right)}=widehat{SBA}=60{}^circ ;AC=2a$
$Rightarrow SA=ABsin 60{}^circ =asqrt{3}.$
Dựng $DEbot AC$$left( Ein BC right)$ tại I, mặt khác $DEbot SARightarrow DEbot left( SAC right)Rightarrow DEbot SC$. Dựng $IHbot SC$
$Rightarrow SCbot left( EHD right)$. Ta có: $DI=DCsin widehat{ICD}$ trong đó $tan widehat{ICD}=sqrt{3}Rightarrow widehat{ICD}=60{}^circ .$
Suy ra $DI=asin 60{}^circ =frac{asqrt{3}}{2};DE=frac{D{{C}^{2}}}{DI}=frac{2a}{sqrt{3}}.$
$Rightarrow IE=DE-DI=frac{asqrt{3}}{6}Rightarrow CI=sqrt{EI.DI}=frac{a}{2};sin widehat{ICH}=frac{SA}{SC}=frac{sqrt{3}}{sqrt{7}}Rightarrow IH=ICsin widehat{IHC}=frac{asqrt{3}}{2sqrt{7}}$
Suy ra $EH=sqrt{E{{I}^{2}}+I{{H}^{2}}}=frac{2a}{sqrt{21}};ED=frac{asqrt{42}}{7}.$
Do đó $cos widehat{EHD}=frac{E{{H}^{2}}+H{{D}^{2}}-E{{D}^{2}}}{2.EH.HD}=frac{-sqrt{2}}{4}<0Rightarrow cos widehat{left( left( SBC right);left( SCD right) right)}=frac{sqrt{2}}{4}.$
| Bài tập 5: Cho hình chóp S.ABCD có đáy là hình vuông tâm O, cạnh a. Biết $SAbot left( ABCD right)$, tính độ dài đoạn thẳng SA để góc giữa mặt phẳng (SBC) và (SCD) bằng $60{}^circ $. |
Lời giải chi tiết
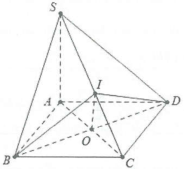
Ta có: $left{ begin{array} {} BDbot AC \ {} BDbot SA \ end{array} right.Rightarrow BDbot left( SAC right)Rightarrow BDbot SC.$
Kẻ $BIbot SCRightarrow SCbot left( BID right).$
Vậy $widehat{left( left( SBC right);left( SCD right) right)}=widehat{left( BI;ID right)}=60{}^circ .$
Dễ thấy $left{ begin{array} {} OIbot SC \ {} widehat{BIO}=frac{1}{2}widehat{BID} \ end{array} right..$
■ Trường hợp 1: $widehat{BID}=60{}^circ Rightarrow widehat{BIO}=30{}^circ .$
Ta có: $tan widehat{BIO}=frac{BO}{IO}=tan 30{}^circ Rightarrow OI=frac{asqrt{6}}{2}>OC=frac{asqrt{2}}{2}$ (vô lý).
(OI là cạnh góc vuông, OC là cạnh huyền của tam giác vuông OIC).
■ Trường hợp 2: $widehat{BID}=120{}^circ Rightarrow widehat{BIO}=60{}^circ .$
Ta có: $tan widehat{BIO}=frac{BO}{IO}=tan 60{}^circ Rightarrow OI=frac{asqrt{6}}{6}.$
Mặt khác: $sin widehat{ICO}=frac{OI}{OC}=frac{sqrt{3}}{3}Rightarrow tan widehat{ICO}=frac{1}{sqrt{2}}Rightarrow SA=ACtan widehat{ICO}=a.$
| Bài tập 6: Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều cạnh a với $AB=2a$, biết rằng $SAbot left( ABCD right)$ và $SA=asqrt{3}$. Tính tan góc giữa 2 mặt phẳng (SAB) và (SCD). |
Lời giải chi tiết
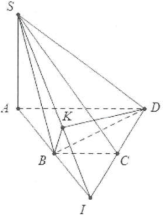
Do ABCD là nửa lục giác đều cạnh a với $AB=2aRightarrow $ABCD nội tiếp đường tròn đường kính AB. Do đó $widehat{ABD}=90{}^circ .$
Gọi $I=ABcap CDRightarrow SI=left( SAB right)cap left( SCD right).$
Do $left{ begin{array} {} AIbot BD \ {} BDbot SA \ end{array} right.Rightarrow BDbot left( SAI right)Rightarrow BDbot SI.$
Dựng $BKbot SIRightarrow SIbot left( BKD right).$
Khi đó $widehat{left( left( SAB right);left( SCD right) right)}=widehat{left( BK;KD right)}=widehat{BKD}.$
Do $BDbot left( SAI right)Rightarrow BDbot BKRightarrow Delta KBD$ vuông tại B có $BD=sqrt{A{{D}^{2}}-A{{B}^{2}}}=asqrt{3}.$
Do $left{ begin{array} {} BC//AD \ {} BC=frac{1}{2}AD \ end{array} right.Rightarrow $ BC là đường trung bình trong tam giác $AIDRightarrow AB=BI$ và $AI=2a$
$Rightarrow BK=frac{1}{2}dleft( A;SI right)=frac{1}{2}.frac{SA.AI}{sqrt{S{{A}^{2}}+A{{I}^{2}}}}=frac{asqrt{21}}{7}Rightarrow tan widehat{BKD}=frac{BD}{BK}=sqrt{7}.$