Cho tứ diện (OABC) có (OA,OB,OC) đôi một vuông góc với nhau. Kí hiệu (S,{S_1},{S_2},{S_3}) lần lượt là diện tích các tam giác (ABC,OAB,OBC,OCA). Chứng minh rằng
(frac{{S_1^2}}{{2S_1^2 + {S^2}}} + frac{{S_2^2}}{{2S_2^2 + {S^2}}} + frac{{S_3^2}}{{2S_3^2 + {S^2}}} le frac{3}{5}).
Lời giải
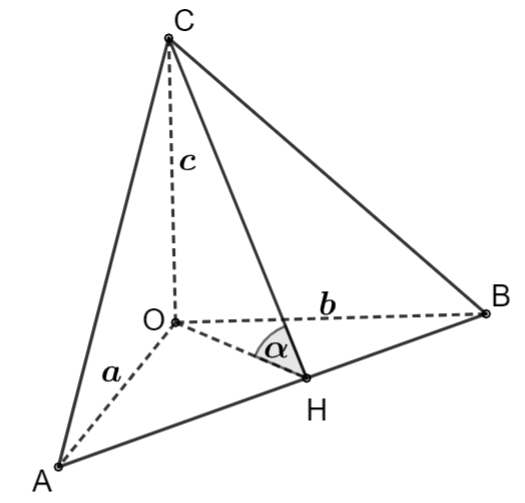
Đặt (OA = a,OB = b,OC = c). Gọi (H) là hình chiếu của (O) xuống (AB), (alpha ) là góc giữa (left( {ABC} right)) và (left( {OAB} right)).
Ta có (frac{{{S^2}}}{{S_1^2}} = frac{1}{{{{cos }^2}alpha }} = {tan ^2}alpha + 1 = frac{{{c^2}}}{{{a^2}}} + frac{{{c^2}}}{{{b^2}}} + 1 = frac{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}}}{{{a^2}{b^2}}})
suy ra (frac{{S_1^2}}{{2S_1^2 + {S^2}}} = frac{1}{{2 + frac{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}}}{{{a^2}{b^2}}}}} = frac{{{a^2}{b^2}}}{{3{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}}}).
Tương tự ta có (frac{{S_2^2}}{{2S_2^2 + {S^2}}} = frac{{{b^2}{c^2}}}{{{a^2}{b^2} + 3{b^2}{c^2} + {c^2}{a^2}}}),(frac{{S_3^2}}{{2S_3^2 + {S^2}}} = frac{{{c^2}{a^2}}}{{{a^2}{b^2} + {b^2}{c^2} + 3{c^2}{a^2}}})
Đặt (left{ begin{array}{l}x = {a^2}{b^2}\y = {b^2}{c^2}\z = {c^2}{a^2}end{array} right.) và biểu thức (F = frac{x}{{3x + y + z}} + frac{y}{{x + 3y + z}} + frac{z}{{x + y + 3z}}).
Do (F) là biểu thức thuần nhất nên ta có thể giả sử (x + y + z = 3). Khi đó
(F = frac{x}{{2x + 3}} + frac{y}{{2y + 3}} + frac{z}{{2z + 3}}).
Dễ dàng chứng minh được (frac{x}{{2x + 3}} le frac{{3x + 2}}{{25}}) với mọi (x > 0) (biến đổi tương đương).
Áp dụng cho (x,y,z) ta được
(F le frac{{3x + 2}}{{25}} + frac{{3y + 2}}{{25}} + frac{{3z + 2}}{{25}} = frac{3}{5}).
Dấu bằng xảy ra khi và chỉ khi (x = y = z = 1) hay (a = b = c).
