Câu 1: Cho \(A\), \(B\) là hai biến cố xung khắc. Biết \(P\left( A \right)=\frac{1}{3}\), \(P\left( B \right)=\frac{1}{4}\). Tính \(P\left( A\cup B \right)\). A. \(\frac{7}{12}\). B. \(\frac{1}{12}\). C. \(\frac{1}{7}\). D. \(\frac{1}{2}\). Hướng dẫn giải: \(P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)=\frac{7}{12}\). Câu 2: Một lớp học có 100 học sinh, trong đó có 40 […]
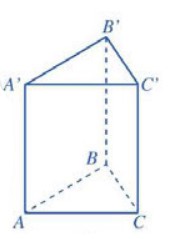
1.1. Hình lăng trụ đứng. Hình lăng trụ đều Định nghĩa – Hình lăng trụ có cạnh bên vuông góc với mặt đáy được gọi là hình lăng trụ đứng. – Hình lăng trụ đứng có đáy là đa giác đều gọi là hình lăng trụ đều. – Hình lăng trụ đứng có đáy là hình bình […]
Câu 1: Tính đạo hàm cấp hai của các hàm số sau: a) \(f(x) = {(2x – 3)^5}.\) b) \(f(x) = \frac{{{x^2} + x + 1}}{{x + 1}}\). Hướng dẫn giải: a) Ta có: \(f'(x) =\left [ \left ( 2x-3 \right )^5 \right ]’= 5.(2x – 3)'{(2x – 3)^4} = 10{(2x – 3)^4}.\) \(f”(x) = \left[ […]
1.1. Một số bài toán dẫn đến khái niệm đạo hàm a) Vận tốc tức thời của một vật chuyển động thẳng Một vật di chuyển trên một đường thẳng (H.9.2). Quãng đường s của chuyển động là một hàm số của thời gian t, s = s(t) (được gọi là phương trình của chuyển […]
1.1. Công thức cộng xác suất cho hai biến cố xung khắc a) Biến cố xung khắc Biến cố A và biến cố B được gọi là xung khắc nếu A và B không đồng thời xảy ra. Hai biến cố A và B xung khắc khi và chỉ khi A \(\cap\) B =\(\emptyset\). […]
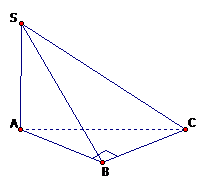
1.1. Thể tích khối chóp Thể tích của khối chóp có diện tích đáy S và chiều cao h là \(V = \frac{1}{3}hS\). 1.2. Thể tích khối chóp cụt đều Thể tích của khối chóp cụt đều có diện tích đáy lớn S, diện tích đây bé S’ và chiều cao h là \(V = […]
1.1. Góc giữa hai mặt phẳng, hai mặt phẳng vuông góc – Cho hai mặt phẳng (P) và (Q). Lấy các đường thẳng a, b tương ứng vuông góc với (P), (Q). Khi đó, góc giữa a và b không phụ thuộc vào vị trí của a, b và được gọi là góc giữa hai […]
1.1. Khái niệm Lôgarit Định nghĩa Cho hai số thực dương a, b với a khác 1. Số thực c để ac = b được gọi là lôgarit cơ số a của b và kí hiệu là \({{\log }_{a}}b\), nghĩa là \(c={{\log }_{a}}b\Leftrightarrow {{a}^{c}}=b\) Tính chất Với số thực dương a khác 1, số thực dương b, ta có: 1) \({{\log }_{a}}1=0\) 2) \({{\log }_{a}}a\,=1\) 3) \({{\log }_{a}}{{a}^{c}}=c\) 4) \({{a}^{{{\log }_{a}}b}}=b\) Lôgarit thập […]
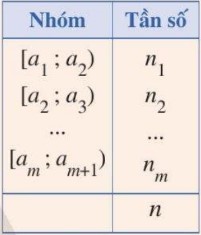
1.1. Mẫu số liệu ghép nhóm a. Bảng tần số ghép nhóm – Mẫu số liệu ghép nhóm là mẫu số liệu cho dưới dạng bảng tần số ghép nhóm. – Mỗi nhóm số liệu gồm một số giá trị của mẫu số liệu được ghép nhóm theo một tiêu chí xác định có dạng [a; b), […]
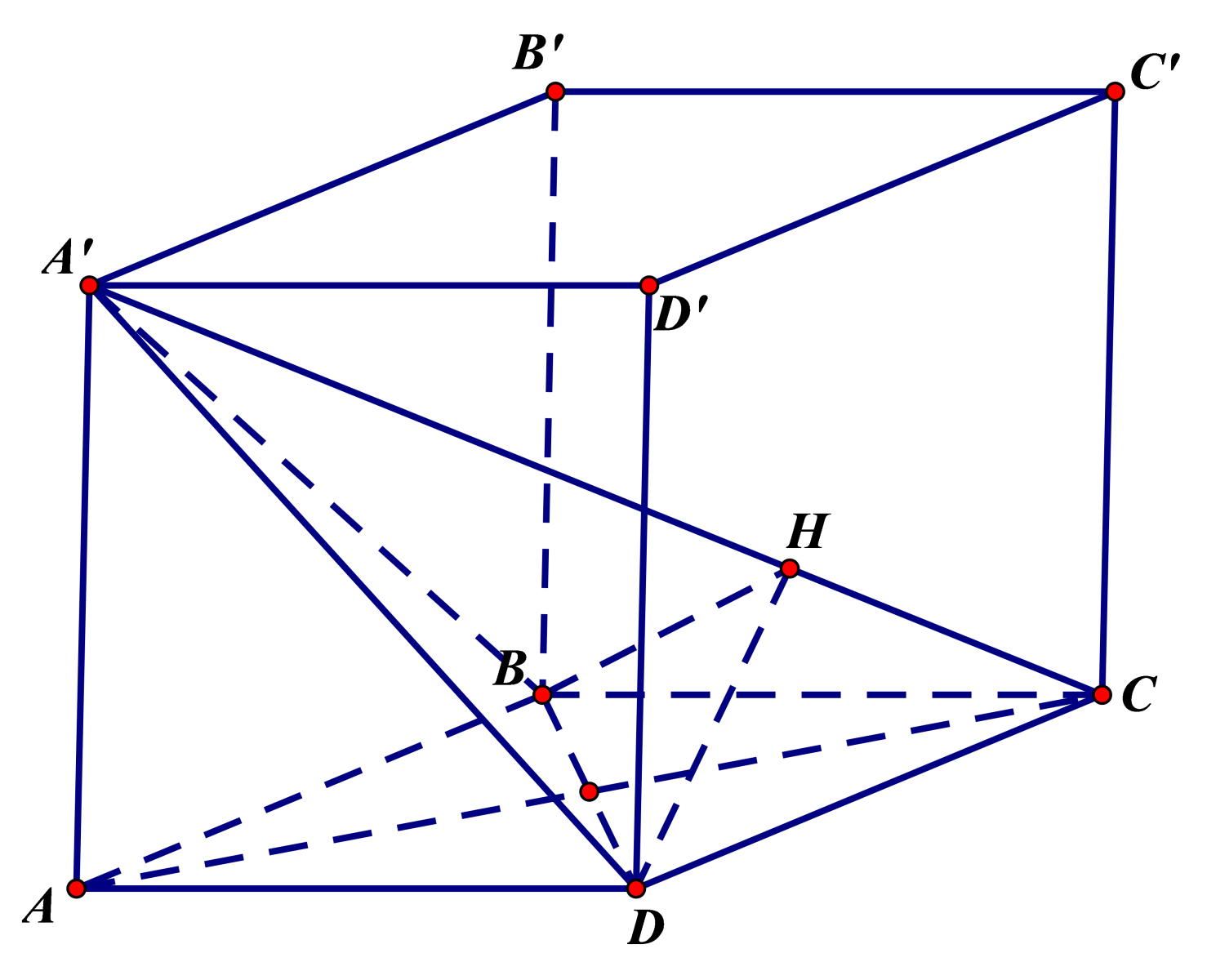
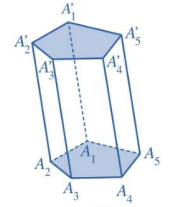
LÝ THUYẾT TÓM TẮT 1.1. Hình lăng trụ a. Định nghĩa Hình gồm hai đa giác A1A2…An, A1’A2’…An’ và các hình bình hành A1A2A2’A1’, A2A3A3’A2’, …, AnA1A1’An’ được gọi là hình lăng trụ, kí hiệu là A1A2…An.A1’A2’…An’. Chú ý: Nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác,… thì hình lăng […]